Varukorg Minimera varukorgen
| SEK SEK EUR EUR |
| Rabatt | - EUR | - SEK |
| Summa | EUR | SEK |
| Frakt | EUR | SEK |
| Moms | EUR | SEK |
| Totalt | EUR | SEK |
Varukorg Minimera varukorgen
| SEK SEK EUR EUR |
| Rabatt | - EUR | - SEK |
| Summa | EUR | SEK |
| Frakt | EUR | SEK |
| Moms | EUR | SEK |
| Totalt | EUR | SEK |
Här publiceras frågor och svar som ska vara till hjälp för dig som arbetar med tillämpningen av standarden för betongskonstruktioner.
Fråga publicerad 2023-02-08.
Fråga:


Svar:

Fråga publicerad 2023-02-08.
Fråga:

Svar:





Fråga publicerad 2023-02-08.
Fråga: Ni har tidigare svarat på en fråga om bockningsradie. Där svarade ni att alla tre strecksatser under 8.3 inte behövde vara uppfyllda. Detta skulle vara oklart formulerat i tidiga utgåvor, enligt svaret. Men var i gällande standard framgår det nu tydligt att de tre strecksatserna inte behöver vara uppfyllda? Räcker det att en strecksats är uppfylld? Eller ska minst två vara uppfyllda?
Svar: Av SS-EN 1992-1-1:2005/AC:2010 (Sv) och ändring nr. 101 framgår att antingen första eller andra strecksatsen gäller. Tredje strecksatsen gäller alltid
Fråga publicerad 2023-01-09.
Fråga: I svaret på en fråga publicerad 2021-11-03 om bockningsdiametrar för byglar anges att inte alla strecksatserna i 8.3 måste vara uppfyllda. Var i gällande normer kan jag finna att alla tre strecksatser i 8.3 inte behöver vara uppfyllda? Räcker det med en strecksats, eller krävs det att två är uppfyllda? Vilka strecksatser kan i så fall kombineras?
Svar: I ett Corrigendum som utgavs för mer än 12 år sedan gjordes en ändring som innebar att antingen den första eller den andra strecksatsen skulle uppfyllas. Denna ändring är dock inte införd i gällande svenska översättning; för att hitta den måste man därför gå till SS-EN 1992-1-1:2005/AC:2010 (Sv) och ändring nr. 101. Den tredje strecksatsen är egentligen onödig, eftersom bockningsdiametern alltid måste vara minst enligt tabell 8.1N för att undvika skador på stången, oavsett inverkan på betongen.
Fråga publicerad 2023-01-04.
Fråga: Har en fråga angående robusthetskrav på koppling mellan bjälklag och vägg. I kap 9.10.2.4. står att vägg bör förankras till bjälklaget för en kraft på 20 kN/m. Om bjälklag spänner i en riktning, tex med HDF så finns det ofta väggar orienterade parallellt med bjälklagsplattor som inte tar ner vertikallast. Behöver dessa "icke-bärande" väggar även kopplas samman med minst en kraft på 20 kN/m? Frågan gäller i de fall stabilisering uppnås även vid bortfall av en enskild vägg som ej bär bjälklag
Svar: Varken EN 1992-1-1 eller EKS klargör att reglerna bara gäller bärande eller stabiliserande väggar, och anger inte heller undantag för väggar som inte stabiliserar eller bär bjälklag. Det hela är därför lite oklart.
En rimlig tolkning är dock att reglerna endast behöver tillämpas för bärande och/eller stabiliserande väggar, eftersom bortfall av vägg som varken bär bjälklag eller stabiliserar knappast kan medföra ett fortskridande ras.
Fråga publicerad 2023-01-04.
Fråga: Är det möjligt att ta hjälp av friktion för att nå upp till tillräcklig kapacitet för kopplingar med avseende på robusthet. Om det till exempel finns krav på att balk och kantpelare ska knytas ihop för en kraft vinkelrätt balkriktning på 150 kN. Skulle det då vara möjligt att dela upp kraften så att viss kraft tas av friktion, eller måste hela kraften tas av en mekanisk koppling. Frågan gäller också förr förankring inre dragband mellan bjälklagsplatta och vägg
Svar: Armering och kopplingar för att förhindra fortskridande ras handlar till stor del om att ge konstruktionen en viss seghet, förutom att kopplingar och armering ska kunna ta vissa krafter. Olyckslaster innebär dessutom i regel någon form av stötkraft, vilket innebär att tredje strecksatsen i En 1992-1-1 10.5.1 (2) utesluter utnyttjande av friktion.
Friktion kan alltså inte utnyttjas för att ta upp krafter som är till för att ge robusthet.
I EKS 11 anges dessutom att bilaga A i SS-EN 1991-1-7 ska tillämpas på byggnader. Och man talar i detta sammanhang om förbindningar och dragband som ska möjliggöra ett segt beteende. Detta understryker att friktion inte kan utnyttjas för att ta de krafter som robusthetskravet anger
Fråga publicerad 2022-11-23.
Fråga: Min fråga berör minimiarmering av betongbjälklag. Mer specifikt fria kanter i bjälklag och balkonger. Enl. EK2 9.3.1.4 ska man ha en armering vid fri kant. Jag tolkar detta som en princip, dvs något vi ska ha med. Det som är oklart, är hur mkt armering som behövs. Denna typ av armering fanns inte i BBK men tillkom i Eurokoden. Hur mycket armering ska läggas in då det inte framgår av reglerna? Och hur ska detta tolkas för balkonger? Gäller samma sak för balkongers fria kant som för ett bjälklags fria kant? Ett svar på en tidigare fråga till Eurokod Helpdesk SS-EN 1992-1-1- Armering i balkongplattor väcker fler frågor då vi tolkar detta som att armeringen finns enbart som montagearmering. Om det skulle vara så att ni anser att man ska ha armering den i fria kanten, kan balkongproducenter välja att frångå kravet i 9.3.1.4 och inte sätta in dessa byglar? Vem ansvarar då för produktens konstruktion och avsteg?
Svar: 9.6.1.4 (1) är ingen princip utan ett allmänt råd, vilket framgår av verbet ”bör”.
Det inte relevant att tillämpa regler för tvärkraftsamering på det aktuella fallet, dels för att dessa gäller plattor med en tjocklek på minst 200 mm, dels för att det i en ensidigt upplagd konsolande balkongplatta knappast uppstår några väsentliga tvärkrafter eller vridmoment som skulle kräva armering enligt figur 9.8.
I två- eller tresidigt upplagda balkongplattor kan dock såväl tvärkraft som vridmoment uppstå längs den fria kanten, och i så fall bör minimiarmering i form av byglar läggas in, förslagsvis med samma dimension och delning som för övrig minimiarmering i motsvarande riktning.
Dessutom gäller hela avsnitt 9.3 för enkelspända och flersidigt upplagda plattor, således inte för konsolande balkongplattor (i frågan nämns visserligen även fria kanter i bjälklag men frågan handlar om balkongplattor inspända i bakkanten, dvs konsoler.)
Fråga publicerad 2022-11-23.
Fråga: En följdfråga på fråga/svar SS-EN 1992-1-1 Minimiarmering, fråga 5 publicerad i Eurokod Helpdesk 2019-08-26 samt en fråga om det allmänna rådet i EKS 11 § 23 a.
Minst 25% av minimiarmering i formel 9.1 N ska läggas in i alla betongplattor. Gäller det både under och ovankant oavsett om kanten är tryckt eller dragen?
Gäller en konstruktion i exponeringsklass XC1, livslängdsklass L50, betong C45/55 där man vill undvika sprött brott.
Svar:

Fråga publicerad 2022-11-23.
Fråga: Gäller påkörningslaster även vid mindre byggnader som till exempel en enkel öppen carport av träkonstruktion som skall rymma ett antal bilar? Det känns som dimensionerna blir orimligt stora för en sådan konstruktion om man räknar med den vanliga påkörningslasten. Samtidigt bör stommen ha en viss robusthet. Är det de sedvanliga påkörningslasterna som gäller vid dimensioneringen, eller kan man resonera på något annat sätt, till exempel att man låter en del av stommen rasa vid en påkörning?
Svar: Enligt Boverkets EKS (BFS 2019:1), avd B, kap.1.1.7 § 1 a behöver inte byggnader i konskevensklass 1 i tabell A.1 i bilaga A till SS-EN 1991-1-7 dimensioneras för olyckslaster. Exempel på vilka typer av byggnader det gäller fås i Tabell A.1 8 (svensk version):
Läser man den engelska versionen ser man dock att översättningen inte är helt korrekt. (Detta kommer att påtalas till ansvarig projektledare hos SIS för korrigering). Där står nämligen 1,5 ggr byggnadshöjden, inte halva byggnadshöjden.
Principen är alltså att en carport eller liknande inte behöver dimensioneras för olyckslast (till exempel påkörning) utan tillåts kollapsa om detta inte leder till att en annan byggnad där människor vistas skadas av denna kollaps. Om kollapsen kan leda till risk för att människor som befinner sig på någon annan typ av yta där människor vanligtvis samlas eller många befinner sig på, så bör man dimensionera för olyckslast eller via en riskbedömning komma fram till om man kan vidta andra skyddsåtgärder. Det gäller om den andra byggnaden eller ytan befinner sig inom avståndet 1,5 ggr carportens höjd från carporten.
Det kan även nämnas att för kända olyckslaster är det enligt EKS avd. B, kap.1.1.7 tillåtet att använda metoden med lokalt brott. Kravet är att området som kollapsar inte får vara större än det minsta av 15 % av bjälklagsarean eller 100 m2 i vardera av två angränsande plan. Mer information finns i Boverkets vägledning om olyckslaster, Olyckslaster - PBL kunskapsbanken - Boverket.
Fråga publicerad 2022-02-21.
Fråga: Går det att komma runt kravet på minimiarmering i hög balk på något sätt när man inte tycker det är relevant?
Ett konkret exempel: En vägg med en fönsteröppning som är 1210 mm bred och med ett 3200 mm högt överstycke över fönstret. Det är beskedliga laster på väggens överkant? Det känns inte motiverat med minarmering både vertikalt och horisontellt. Går det att på något sätt verifiera/bevisa att det inte är nödvändigt med minarmering? Om det trots allt måste in minarmering; räcker det om vertikala stänger förankras förbi den övre trycksträvan eller måste vertikala armeringen gå hela vägen upp till väggens överkant?
Svar: Är siffrorna korrekta: 3200 mm = 3,2 m högt överstycke?
Om det är rätt så är ju exemplet ganska extremt, och i ett sådant fall kan man kanske påvisa att de dragspänningar som behövs för jämvikt ligger under draghållfastheten för oarmerad betong enligt kapitel 12 och EKS, och då kan man undvara minimiarmering.
Reglerna för minimiarmering är ju i första hand tänkta för höga balkar som är beroende av armering för sin jämvikt.
Fråga publicerad 2021-11-03.
Fråga: I tabell 8.1N. är dorndiameter för bockning av stänger och trådar klart angivet, men det är något oklart vad som gäller för byglar. Är det dorndiametern i figur 8.1b som gäller för byglar eller gäller samma dorndiameter som i gamla BBK 04?
Svar: Byglar består ju av stänger eller trådar, så där är det ingen principiell skillnad. Däremot är det ju så att byglar vanligen har en minst lika grov hörnstång innanför bocken, vilket innebär att den andra strecksatsen i 8.3 (3) då är uppfylld och att ekvation (8.1) inte behöver användas. Alla tre strecksatserna behöver inte vara uppfyllda, vilket kan vara oklart i tidiga utgåvor av SS-EN 1992-1-1.
Observera också att tabell 8.1N i Sverige i de flesta fall kan ersättas med det allmänna rådet för SS-EN 1992-1-1, 8.3.2 som finns i 23§, Avd D i EKS 11. EKS 11.
Fråga publicerad 2021-07-16.
Fråga:
Hej, Jag undrar över om man behöver byglar för de fria kanterna för en "oarmerad" vägg där man har armering även om den inte är nödvändig med hänsyn till bärförmågan? Enligt 9.6.3 (1) anges det att man ska ha As,hmin på alla ytor och med de fria kanterna. Enligt EKS 11 9.6.2(1) finns ingen undra gräns för Asv,min för väggar med h/b mindre än 18, dock ska man alltid använda 25 % av den vertikala armering enligt EKS11 9.6.3(1). Bör man då lägga in byglar vid de fria kanterna och varför?
Illustrerar med tre exempel enligt nedan, där det ligger armering i väggen av andra anledningar än den med hänsyn till bärförmåga för väggen, exempelvis för ingjutningsgods eller för att förhindra krymp och krypsprickor. Överst ligger dock en armering för att förhindra hörnspjälkning på grund av punktlasten.

Svar:

Fråga publicerad 2021-07-16.
Fråga:

Svar:

Fråga publicerad 2021-07-16.
Fråga:

Svar:


Fråga publicerad 2021-07-08.
Fråga: I SS-EN 1992-1-1 stycke 6.5.4 anges den dimensionerande tryckspänningen i ekv (6.60), (6.61), (6.62) där faktorn k ger en reduktion beroende på om dragband förankras eller ej och om dessa är förankrade i en riktning eller flera. Hur man ska tänka när det gäller exempelvis ett pålfundament med tre pålar? Den tryckta strävan som bildas mellan pålen och en pelarlast utbreds på en yta där dragband korsar varandra i olika riktningar. Hur ska man tänka för att beräkna ytan som tryckkraften angriper på för att få ut spänningen om man har ett pålfundament med tre pålar där armering ligger uppe på pålskallarna och bildar 60-gradersvinklar mot varandra (sett i plan)? Figur 6.28 i SS-EN 1991-1-1 inte motsvarar detta fall. Denna nod borde vara en CCTT-nod, det vill säga noden tar dragkraft från de olika riktade armeringsstängerna och tryckkraft från påle respektive betongsträva. Vad gäller det för reduktionsfaktor här, är det fortfarande k3=0,75?
Svar: Det fall som ligger närmast till hands är figur 6.27, som visar en så kallad CCT-nod där två trycksträvor balanseras av ett dragstag. I detta fall är det visserligen två dragstag i olika riktningar, vilket möjligen är lite sämre, men detta fall är inte definierat. Figur 6.28 visar visserligen två dragstag i olika riktningar, men skillnaden mot 6.27 är att det då är en trycksträva som balanseras av två dragstag. Därför föreslås att använda 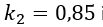
Den vertikala tryckspänningen vid pålhuvudet blir helt enkelt pålkraften dividerat med pålhuvudets area. När det gäller tryckspänningen i den lutande trycksträvan finns ingen direkt vägledning i SS-EN 1992-1-1 för detta fall, men man skulle kunna göra en utvidgad tolkning av figur 6.27 enligt nedanstående förslag, se figur nedan:

Om armeringen ligger direkt på pålhuvudet är och .
Vidare gäller
Det kan tilläggas att om armeringen kan utformas och förankras på ett sådant sätt att den inte passerar genom nodområdet, så kan man se noden som en CCC-nod, med 
Fråga publicerad 2021-04-12.
Fråga: Jag undrar över om man behöver byglar för de fria kanterna för en "oarmerad" vägg där man har armering även om den inte är nödvändig med hänsyn till bärförmågan? Enligt 9.6.3 (1) anges det att man ska ha As,hmin på alla ytor och med de fria kanterna. Enligt EKS 11 9.6.2(1) finns ingen undra gräns för Asv,min för väggar med h/b mindre än 18, dock ska man alltid använda 25 % av den vertikala armering enligt EKS11 9.6.3(1). Bör man då lägga in byglar vid de fria kanterna och varför?
Illustrerar med ett exempel enligt nedan, där det ligger armering i väggen av andra anledningar än den med hänsyn till bärförmåga för väggen, exempelvis för ingjutningsgods eller för att förhindra krymp och krypsprickor. Överst ligger dock en armering för att förhindra hörnspjälkning på grund av punktlasten.
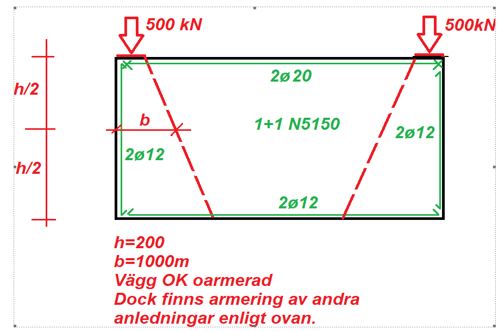
Svar:

balkar kan normalt inte göras oarmerade, och för minimiarmering gäller nu i stället avsnitt 9.7. Det ska då finnas rutarmering med viss mängd på båda sidorna. Dragbandet ser ut att vara förankrat i noderna, vilket är bra.
Fråga publicerad 2021-04-12.
Fråga: När man läser kapitel 9.10.2.3 Inre dragband, så är det oklart huruvida det ska finnas dragband längs alla bärande väggar, eller om det räcker med att lägga kontinuerliga dragband (ut till fasad) vid vissa av dessa väggar? Enligt information på ett seminarium kunde det tolkas som att ska lägga in armering längs alla bärande inre väggar. Kan det vara olika typ av armering som avses?
Svar: Inre dragband kan antingen koncentreras längs bärande inre väggar (eller balkar), eller fördelas över plattornas bredd när så är möjligt. Om de koncentreras längs väggar (eller balkar), vilket är det vanligaste, så gäller det normalt alla bärande väggar (eller balkar). I princip kan man dock tänka sig att dragbanden är koncentrerade längs vissa väggar (balkar) och fördelade i andra områden.
Den totala kraft som ska klaras av ett dragband som är associerat med en viss vägg, antingen dragbandet är koncentrerat eller fördelat i plattan, är proportionell mot halva avstånden till närliggande väggar, med en undre gräns på 70 kN per vägg. Så länge inte den undre gränsen är avgörande spelar det då ingen roll för den totala kraften om dragbanden är koncentrerade eller fördelade.
Fråga publicerad 2021-04-12.
Fråga: Figur 6.21N anger approximativa värden på βatt använda vid kontroll av genomstansning. I avsnitt 6.4.3 (6) står att dessa får användas när sidostabiliteten inte bygger på ramverkan och när längder på angränsande spann inte avviker mer än 25 %. Villkoret kring spannlängder är lätt att förstå när det gäller till exempel pelardäck. Men vad gäller för en platta med bara ett spann i vardera riktningen? Ska spannlängderna i de olika riktningarna jämföras? Eller blir användning av figur 6.21N direkt OK alternativt EJ OK? Frågeställningen kan bli aktuell för exempelvis en rektangulär avlång platta med en påle i varje hörn. Tillåts då direkt β= 1,5 eller krävs det noggrannare beräkning?
Svar: För en platta med bara ett spann i vardera riktningen borde man kunna använda β = 1,5 . Att jämföra spannlängderna i de båda riktningarna är knappast relevant. Det borde snarare vara gynnsammare om dessa längder är olika än om de är lika.
Fråga publicerad 2021-03-01.
Fråga:
1) I SS-EN 1992-1-1, 7.3.4 finns en formel som används för sprickbreddberäkning vid förhindrad krympning. Gäller denna formel även för sprickor som beror på inre tvång i betongkonstruktioner? Som vid temperaturökning under härdningsprocessen.
2) Gäller eurokoden regler när det gäller sprickbreddberäkningar och miniminarmering på grund av sprickbreddskrav även för förtillverkade element? Eller är det så att man måste kontrollera sprickbredd vid lastförhållanden, men inte vid till exempel krympning?
3) Finns det några riktlinjer vad gäller ju krympning för förtillverkade element?
Svar:
1) Metoden i EN 1992-1-1 7.3.4 är i första hand avsedd för beräkning av sprickbredd vid armeringstöjning orsakad av last. Den är således inte lämpad för sprickor på grund av förhindrad krympning eller inre tvång, om vid temperaturökning vid härdning. För sprickor på grund av förhindrad krympning eller annan tvångsinverkan hänvisas i stället till EN 1992-3, bilaga L och M.
2) Eurokoden gäller för förtillverkade element i lika hög grad som för platsgjutna konstruktioner. För förtillverkade element som kan utsättas för sprickbildning på grund av tvång gäller således samma krav på minimiarmering för sprickbreddsbegränsning. Å andra sidan kan ju förtillverkade element i allmänhet vara mindre utsatta för sådan tvångsinverkan. Det är konstruktörens ansvar att göra den bedömningen från fall till fall; eurokoden säger ingenting särskilt om detta. Sprickbreddskontroll med hänsyn till krympning är aktuell om elementet kan utsättas för tvång på grund av förhindrade krymprörelser, annars inte.
3) Det finns inga riktlinjer som specifikt handlar om krympning hos förtillverkade element. Om ett förtillverkat element monteras så att det blir fastlåst, t.ex. längs en kant, eller vid motsatta kanter, så kan det bli fråga om tvång enligt figur L.1 (a) respektive (b) i EN 1992-3. Om elementet inte har "krympt färdigt" så kan det uppstå tvång på grund av förhindrade krymprörelser. Sådana situationer torde vara sällsynta, men inte omöjliga, och i så fall kan det bli aktuellt med sprickfördelande armering och sprickbreddsbegränsning. Det är upp till konstruktören att bedöma detta från fall till fall.
Det bör påpekas att minimiarmering kan behövas av andra skäl än för sprickbreddsbegränsning, se kapitel 9. Där handlar det istället om vilken bärande funktion elementet har: som balk, platta, pelare, hög balk, vägg (som dock kan utföras oarmerad) med mera. I det fallet finns det inget som skiljer förtillverkat från platsgjutet.
Fråga publicerad 2021-02-03.
Fråga: Hur skall andra ordningens moment beräknas i bruksgränstillståndet för pelare/väggar? Om man väljer styvhetsmetoden ska man då beräkna enligt ekvation 5.28 men med styvheten EI beräknad på vanligt sätt med hänsyn till krypning och uppsprickning? Ekvation 5.21 gäller väl bara för brottgränstillståndet? Hur gör man i bruksgränstillståndet om man väljer krökningsmetoden? I brottgränstillståndet används dimensioneringsvärdet på töjningen vid krökningsberäkningen men om man då i bruksgränstillståndet använder det karakteristiska värdet på töjningen blir ofta krökningen större i bruksgränstillståndet än i brottgränstillståndet, även om man tar hänsyn till skillnaden i normalkraftens storlek. Detta verkar inte rimligt.
Svar: Varken styvhets- eller krökningsmetoden är lämpade för bruksgränstillstånd. De är enbart kalibrerade och avsedda för brottgränstillstånd.
Med styvhetsmetoden avses då sättet att beräkna en nominell styvhet enligt 5.8.7.2. Ekvationerna 5.28 och 5.30 är egentligen inte specifikt knutna till styvhetsmetoden, även om de råkar stå under rubriken 5.8.7. De bygger på allmän statik, och kan därför användas så snart man har en böjstyvhet och motsvarande knäckningslast.
Om man har behov av att beräkna andra ordningens moment i bruksgränstillstånd kan man beräkna styvhet för elastiska förhållanden, med betongens E-modul reducerad för krypning, dvs dividerad med (1+ φ) . Om lasten innehåller korttidslast utöver långtidslast kan man använda ett effektivt kryptal i princip enligt ekvation 5.19.
Böjstyvheten kan påverkas av uppsprickning, vilket i så fall måste beaktas. Det finns ingen färdig formel för styvheten i sprucket tvärsnitt med båda normalkraft och moment, utan här fordras iteration. Även i osprucket tvärsnitt kan det löna sig att beakta armeringens inverkan.
Fråga publicerad 2021-02-03.
Fråga: Min fråga gäller tvärkraftsbrottmoden hävstångsbrott i betong, kapitel 7.2.2.4. För brottmoderna betongkonsbrott (7.21.4) och betongkantbrott (7.2.2.5) ges möjlighet att höja bärförmågan genom att lägga in kompletterande armering. Kontroll av betongen utgår då och ersätts av kontroller av den kompletterande armeringen. Ingen sådan möjlighet att armera mot brottmoden verkar finnas för hävstångsbrott i betong. Bärförmågan reduceras i stället vid förekomst av armering. Dels genom faktorn 0,75 i ekvation 7.39b vid förekomst av kompletterande armering och dels möjligen vid förekomst av ytarmering genom faktorn Ψre,N i beräkningen av NRk,c. Är detta rätt uppfattat? Och är det i så fall inte märkligt att bärförmågan med hänsyn till hävstångsbrott i betong beror av bärförmågan med hänsyn till betongkonsbrott, men att armering som i praktiken höjer bärförmågan med hänsyn till betongkonsbrott sänker bärförmågan med hänsyn till hävstångsbrott i betong? Är det möjligt att NRk,c.i ekv. 7.39b egentligen skulle ersättas med en bärförmåga relaterad till den kompletterande armeringen? Borde inte armering rätvinkligt mot ytan höja bärförmågan? Den höjer ju i praktiken bärförmågan med hänsyn till betongkonsbrott, och bärförmågan med hänsyn till hävstångsbrott i betong är ju beroende av denna.
Vad gäller för kompletterande armering placerad i rät vinkel mot betongytan, alltså armering för drag placerad som 1 (extra armering) i figur 7.2a.
Svar: Det förutsätts att den kompletterande armering som åsyftas ligger rumt infästningen enligt figur 7.10 och parallellt med betongytan. I fallet hävstångsbrott enligt tabell 7.5 har sådan armering ingen positiv inverkan på bärförmågan, vilket möjligen kan förstås med ledning av tabellens illustration. Försök har visat att sådan armering t.o.m. kan ha en negativ inverkan, vilket man har beaktat genom reduktionen med 0,75. är densamma i 7.2.2.4 och 7.4.2.4. Det är svårt att förklara teoretiskt varför kompletterande armering (supplementary reinforcement) i kraftens riktning kan ha en negativ inverkan, men reduktionen bygger på vissa försöksresultat, som man valt att tolka konservativt för olika fall. Reduktion med faktor 0,75 är alltid aktuell vid hävstångsbrott i betong och förekomst av kompletterande armering i kraftens riktning.
Armering placerad rätvinkligt mot betongytan (och därmed även mot kraften) skulle möjligen kunna ha en positiv inverkan, men det ges ingen beräkningsmodell för detta.
Fråga publicerad 2021-02-03.
Fråga: Hur bör man tolka kravet på As,dbmin från 9.7 (1) och hur man kan räkna den armering som ingår i As,dbmin?
Generellt för väggar brukar man tolka det så att den angivna totala mängden kan fördelas jämnt på två sidor, se 9.6.2 (2). I 9.6.3 (1) står inget, men här görs samma tolkning, vilket även finns under era fråga/svar. Hur är det när det gäller höga balkar? Här anges det värdet 0,1% eller 150 mm2/m i varje yta och i vardera riktning. Vilket av följande tre alternativ är en korrekt tolkning av detta?
Alt 1: 0,1% kan fördelas jämnt på varje yta (som för väggar i övrigt) men dock minst 150 mm2/m som också kan fördelas på varje yta (dvs 75 mm2/m / yta).
Alt 2: 0,1% kan fördelas jämnt på varje yta (som för väggar i övrigt) men dock minst 150 mm2/m som ska finnas på varje yta (dvs 300 mm2/m totalt).
Alt 3: 0,1% ska finnas på varje yta (dvs totalt 0,2%) men dock minst 150 mm2/m som ska finnas på varje yta (dvs 300 mm2/m totalt).
Är det okej att summera ihop den armering som finns i den höga balken och sen dela upp den på balkhöjden för att få armering/m för att uppfylla kravet på minsta armering? Om man t.ex. har en vägg som fungerar som en hög balk med tjockleken 200 mm och höjden 3000 mm och armerar den med ett armeringsnät ø5s150 på varje sida så ger det 130 mm2/m. Är kravet 200 mm2/m på varje yta saknas det då ca 70 mm2/m. Om dragbandet utgörs av 2ø16 och man i överkant lägger in 2ø10 så får man utöver nätet (2∙200 m2+2∙78 mm2)/3 = 185 mm2/m, alltså totalt 92 mm2/m extra per sida. Totalt har man då 130+92=222 mm2/m / sida.
Är detta ett felaktigt tolkningssätt för att uppfylla minikraven? Detta uppfyller då givetvis inte rekommendationen på minsta avstånd mellan de grövre järnen, men det kravet klaras av nätet.
Svar: I 9.7 (1) står tydligt att As,dbmin för höga balkar är minst 0,001AC dock minst 150 mm2/m, i varje yta och i vardera riktningen (på engelska in each face and each direction). Det innebär att den totala mängden är minst 0,002AC dock minst 300 mm2/m.
För en hög balk är minimiarmeringen totalt 0,002AC= 400 mm2/m, för det andra gäller detta krav inom alla delar av balken. Ett koncentrerat dragband innebär därför endast att närmaste minimiarmeringsstång kan ligga 300 mm från dragbandet.
Av frågeställarens tolkningar är alternativ 3 korrekt.
För väggar som inte fungerar som höga balkar anges i 9.6.2 (1) och EKS 11 den minsta totala mängden vertikal armering till 0,001AC samt att denna armering, om den är dimensionerande, bör fördelas lika på vardera ytan. Skillnaden mot regeln för höga balkar är att det för väggar inte anges någon undre gräns som motsvarar 150 mm2/m per yta eller 300 mm2/m totalt.
Horisontella dragband i en vägg som inte är en hög balk har inte någon funktion som väggarmering, utan har att göra med antingen skivverkan i bjälklaget eller sammanhållning mot fortskridande ras. De kan därför inte tillgodoräknas som väggarmering.
Minimiarmeringens uppgift är att kunna ta sekundära dragspänningar i betongen på grund av t.ex. lokalt tryck och tvärkraft. Grundprincipen är att den ska vara jämnt fördelad över höjden, och grövre stänger längs kanter bör därför inte medräknas. Koncentrerad armering (dragband) som tar globalt böjmoment är redan dessutom "upptagen" och kan även av detta skäl inte medräknas.
2 Ø10 i överkanten på en 3 m hög väggbalk har ingen sådan funktion, och kan därför möjligen medräknas i minimiarmeringen, åtminstone om det är fråga om samma som hos den övriga minimiarmeringen. Om det handlar om ett dörröverstycke kan dock även överkantsarmeringen vara "upptagen" för att ta inspänningsmoment, och den bör då, av samma skäl som för dragbandet enligt ovan, inte inräknas i minimiarmeringen.
Fråga publicerad 2020-12-18.
Fråga: Ekvation 7.11 i SS8123110:2014 används för att beräkna sprickvidd på grund av enbart tvångsspänningar medan i på 5.8.4(2), Ekv. 5.19 i SS-EN 1992-1-1:2005 beror på moment i bruksgränstillstånd och brottgränstillstånd (SLS/ULS). Vänligen klargör detta.
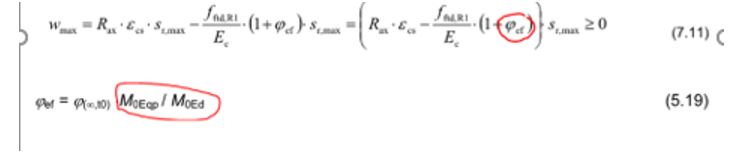
Svar: Det effektiva kryptalet enligt Eurocode 2 (5.19) relateras till böjmoment i SLS/ULS och är avsett att användas för andra ordningens analys, vilket är ett mycket specielllt användningsområde. Det är inte relevant för användning i ekvation 7.11 i SS8123110, som behandlar tvångsspänningar.
Om det inte finns någon specifik definition på effektiv krypning i denna standard, och eftersom denna parameter reducerar den beräknade sprickvidden, ger 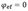
Fråga publicerad 2020-12-15.
Fråga: En fråga angående kontroll av utmattning av armering för vägbroar enligt SS-EN 1992-2, Bilaga NN.2.1. Enligt NN.2.1 (101) så ska utmattningslastmodell 3, enligt SS-EN 1991-2, användas vid denna kontroll. Vid beräkning av korrektionsfaktorn enligt ekvation NN.102, så ska en skadeekvivalent dynamikfaktor, som är beroende av ytans ojämnhet, beaktas. Enligt NN.2.1 (108) är detta en stötfaktor som bestäms enligt EN 1991-2, Bilaga B. I SS-EN 1991-2, Bilaga B (3), framgår det att stötfaktorn kan sättas till 1.2 för ytor med god kvalité och till 1.4 för ytor med medelgod kvalité. Men enligt SS-EN 1991-2, avsnitt 4.6.1 (6), så framgår det att en dynamisk faktor motsvarande beläggning av god kvalité redan ingår i axellasterna för utmattningslastmodellerna 1 t.o.m. 4. Hur går detta ihop med metoden beskriven i SS-EN 1992-2, Bilaga NN.2.1? Är det verkligen rimligt/meningen att den dynamiska faktorn ska beaktas två gånger eller är det en felskrivning?
Svar: För beräkning med avseende på utmattning av vägbroar finns två sätt att bestämma lasterna; endera används lastmodellerna 1 – 4 eller så bestäms lasterna genom uppmätning enligt bilaga B. För själva utmattningsberäkningen finns också två metoder, dels den formella enligt EN 1992-2 i 6.8.7 (med hjälp av bland anna. Wölerkurvor) och dels den förenklade i Bilaga NN. Vid användning av den formella metoden använder man sig endera av utmattningslasterna 1 – 4, där en faktor för vägytans ojämnhet ingår, eller av uppmätta trafikdata enligt Bilaga B till EN 1992-1, och då måste man lägga på en faktor för vägytans ojämnhet.
Metoden i Bilaga NN använder också utmattningslasterna 1 – 4, men då detta är en förenklad metod där beräkningen inte genomförs som en regelrätt utmattningsdimensionering utan med empiriska formler, ska den genomföras enligt de regler som ges i avsnitt NN. Förenklade förfaranden ska ha större säkerhetsmarginal än en beräkningsmetod som är mer verklighetstrogen. Så i det fall man använder Bilaga NN ska den skadeekvivalenta dynamikfaktorn beroende på ytans ojämnhet inkluderas på det sätt som anges, även om det kan tyckas att man redan tagit hänsyn till detta i lastvärdena.
Fråga publicerad 2020-12-15.
Fråga: När det gäller zon-metoden i bilaga B, B.2 i SS-EN 1992-1-2:2004 står det att tvärsnittet ska delas in i parallella zoner med lika tjocklek (rektangulära element), där medeltemperatur och motsvarande medeltryckhållfasthet bestäms för varje zon. Hur tillämpar man detta på temperaturprofilerna från bilaga A för rektangulära pelare?
Svar: I figur B.3 e) (se nedan) visas grundantagandet för hur beräknas för pelare

Fråga publicerad 2020-12-11.
Fråga: BI tabell 5.4 i SS-EN1992-1-2 ökas antingen den totala väggtjockleken eller centrumavståndet till armeringen för att hantera att väggen är exponerad på två sidor istället för en på en sida eller för ökande utnyttjandegrad. För att uppnå brandteknisk klass REI 90 verkar detta logiska angreppsätt inte längre följas. I kolumn 2 anges värdet 120/20 (väggtjocklek/centrumavstånd) för vägg exponerad på en sida medan i kolumn 3 anges värdet 140/10 för vägg exponerad på två sidor. Här ökar alltså den totala tjockleken medan centrumavstånd till armering halveras, trots att väggen nu är exponerad på två sidor. Utgör redovisade värden för täckskikt felaktiga värden för någon av kolumnerna (kolumn 2/3 för REI 90)?
Svar: Här bör man hellre tänka kolumnvis än på hela tabellen som en matris där alla delar hakar i varandra. Tabellen kommer från DIN 4102-4 där en- och tvåsidig brandpåverkan redovisas i separata tabeller vilket gör det mycket svårare att se det du påpekar.
Utan att räkna igenom de enskilda fallen i tabellen går det inte att säga om det är ett fel som smugit in eller om den försvagade armeringen till följd av högre temperaturer kompenseras av att det är mer betong som kan ta tryck. Utgå från att tabellen är rätt även om det ser konstigt ut.
Oavsett vad som står i tabellerna spelar det ingen roll i praktiken om det är 10 eller 20 mm centrumavstånd då kraven på täckskiktets tjocklek i andra delar av Eurokoderna gör att det alltid blir tjockare täckskikt.
Fråga publicerad 2020-12-11.
Fråga: När det gäller dimensionering av oarmerade pelare och väggar gäller kap 12.6.5.2. I SS-EN 1992-1-1:2005A/A1:2014 skall den totala excentriciteten enligt formel 12.12 beräknas även med hänsyn till krypning, eφ. Hur ska denna excentricitet beräknas? Ska den beräknas utgående från ett effektivt kryptal?
Svar: Krypning kan ha mycket stor inverkan på bärförmågan för väggar, i synnerhet för oarmerade sådana. I den ursprungliga modellen i SS-EN1992-1-1:2004, 12.6.5.2 fanns ingen inverkan av krypning, varför modellen kunde ge resultatet mycket på osäkra sidan.
I rättelsen EN 1992-1-1:2004/A1:2014 infördes därför en "krypexcentricitet" att lägga till övriga excentriciteter. Tillägget är dock oanvändbart, eftersom det inte ges någon anvisning om hur det ska beräknas.
I den pågående revideringen EK2 finns andra förslag till modeller för oarmerade väggar, men det är ännu inte klart vad som kommer att väljas.
En alternativ metod att bestämma bärförmågan för oarmerade väggar har presenterats vid en Eurokod 2-konferens i Bratislava 2011.
(Ref: Westerberg, B: Load bearing capacity of unreinforced concrete walls. Conference "Design of concrete structures and bridges", Slovak University of Technology, Bratislava, 12-13 September 2011.)
Denna metod ger mycket god överensstämmelse med generell metod enligt EK2 5.8.6. Den blev dock inte antagen som ersättning för den befintliga metoden vid framtagandet av rättelsen, i stället infördes krypexcentriciteten. "Bratislava-modellen" är därför inte en officiellt godtagen metod, men den används trots detta i viss utsträckning av dem som känner till den, eftersom det inte finns något användbart alternativ (förutom den generella metoden).
Fråga publicerad 2020-12-11.
Fråga: Vid branddimensionering enligt SS-EN 1992-1-2 finns bland annat metod A under kapitel 5.3. I ANM 2 anges att knäcklängden kan reduceras till mellan 50 och 70 % vid mer än 30 minuters brandpåverkan. Gäller detta vid bestämning av NRd och/eller vid den mer noggranna analysen enligt uttrycket (5.7)?
Svar: Enligt 5.3 (3) anges att NRd är dimensionerande bärförmåga vid normala temperaturer och beräknas enligt 1992-1-2 där l0 vid normal temperatur ska användas och inte l0,fi med reducerad knäcklängd.
l0,fi gäller därför enbart för den mer noggranna analysen enligt uttryck 5.7 och ska inte ligga till underlag för verifiering med hjälp av tabell 5.2a.
Fråga publicerad 2020-12-11.
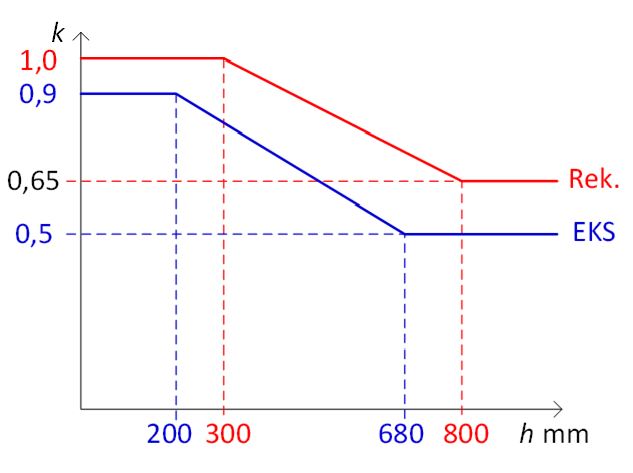
Fråga: Frågan gäller minimiarmering i betong och knyter an till en redan ställd fråga "SS-EN 1992 Avsnitt 7.3.6 minimiarmering för sprickfördelning och inverkan av vct" publicerad 2020-07-01. I svaret till den frågan anges att man i Boverkets EKS har dragit ner värdena på k (0,9 till 0,5 istället för 1,0 till 0,65). Jag undrar var i EKS detta anges? Jag undrar också vilken standard, stycke och formel det är frågan (och svaret) refererar till. Minimiarmering i "vanliga" betongkonstruktioner behandlas i SS-EN 1992-1-1 avsnitt 7.3.2, formel (7.1). Men i frågan anges avsnitt 7.3.6, formel 7.32 som inte existerar i någon av delarna av SS-EN 1992.
Svar: Hänvisningarna till avsnitt och ekvation är felskrivna i fråga 672, så svaret utgår från att det är avsnitt 7.3.2 och ekv (7.1) som avses.
De reducerade värdena på faktorn k anges i EKS 11 Avd D, Kap 2.1.1, $ 4 a.
Fråga publicerad 2020-12-08.
Fråga: Vad är bakgrunden till att faktorn c∙fctd tillåts utnyttjas i tex. vertikala fogar med förtagningar i förtillverkade väggelement? Enligt 6.2.5 (4) så bör c sättas till 0 om fogen kan ha "betydande sprickor", medan man för förtagningar kan använda 0,5. Varför får man använda c om det finns "betydande sprickor"? Om fogen har en spricka är det väl inte troligt att betongens bindande förmåga ger något tillskott. Vad menas med "betydande sprickor"? Finns det någon vägledning för det? Det uppstår alltid rörelse av exempelvis krypning eller temperaturvariationer. Klassas sprickor som uppstår av dessa rörelser som betydande? Om man tar ett väggelement som är 8 m långt som kan krympa helt fritt som exempel. Med en antagen slutkrympning på 0,5 promille fås en krympning på 4 mm under dess livslängd. Man kanske kan anta att ca 30-50 % av denna krympning sker innan elementen monteras och foggjuts, och att man vid fortsatt montering av element får ett tvång av det undre respektive det övre bjälklaget som göt att elementet kommer att krympa? Erfarenhetsmässigt ser man ofta sprickor just i väggfogarna, oberoende av om de har förtagning eller inte och då är det ju intressant att veta hur man ändå motiverar att c får användas.
Svar: c-faktorn bör inte uppfattas alltför bokstavligt som en vidhäftning. Den är, tillsammans med m, ett sätt att anpassa ett enkelt samband till försöksresultat med stor spridning. Följande figur kan användas som förklaring (där ringarna inte är verkliga försöksresultat utan bara en illustration):

I en fog med förtagningar kommer dessa att haka i varandra även om fogen öppnat sig någon mm. Därför kan viss skjuvkraft överföras även om det inte finns vare sig armering eller yttre tryck över fogen, och sambandet kan då börja på en nivå över noll, som i beräkningsmodellen definierats till c∙fctd .
I tidigare svenska normer fanns ett liknande samband, men det började alltid på noll, vilket då kompenserades av en brantare lutning, dvs ett högre värde på μ. Man hade då valt en annan förenklad modell för att anpassa sig till försöksresultat.
Vad som ska ses som "betydande sprickor" är svårt att definiera, men med förtagningar som uppfyller de geometriska villkoren i figur 6-9 bör några enstaka mm inte vara något problem. För fogar utan förtagningar kan man vid val av c-värde ta hänsyn till hur stor del av fogen som är sprucken, samt sprickbredden i förhållande till fogytans eventuella skrovlighet.
Fråga publicerad 2020-11-26.
Fråga: Vad är skillnaden mellan täthetsklass 2 och 3 när det gäller dimensioneringskrav?
Svar:
Från EN 1992-3:
Täthetsklass 2: Läckage bör begränsas. Vissa fuktfläckar accepteras.
Sprickor som kan väntas bli genomgående bör i allmänhet undvikas såvida inte lämpliga åtgärder vidtas (till exempel införande av tätskikt eller fogband)
Täthetsklass 3: Inget läckage tillåts. I allmänhet fordras speciella åtgärder för att säkerställa
vattentäthet (till exempel tätskikt eller förspänning)
Den grundläggande skillnaden mellan 2 och 3 är krav på "begränsat läckage" respektive "inget läckage".
Kraven i täthetsklass 2 kan uppfyllas genom att undvika genomgående sprickor eller genom att förse konstruktionen med tätskikt eller fogband.
För täthetsklass 3 krävs det normalt särskilda åtgärder som tätskikt eller förspänning. Att undvika genomgående sprickor är inte tillräckligt.
Fråga publicerad 2020-11-26.
Fråga: Får man stabilisera förtillverkade betongväggar i ett betonghus i konsekvensklass 2a utan dubb? Enligt 10.5.1 (2) får totalstabiliteten inte enbart bero på friktionen. Får man överföra de horisontella lasterna i undergjutningen med vidhäftning? (Ekv 6.25) Vidhäftningen och friktion är närbesläktade. Regeln i 10.5.1 (2) säger att man inte bör förlita sig på enbart friktion i de fall som räknas upp, även om detta skulle räcka. Här är den sista strecksatsen svår att undkomma; risk för stötkrafter finns ju alltid där det kan förekomma påkörning, om inte annat i garage.
Svar: Detta innebär att man bör ha någon annan typ av kraftöverföring utöver "friktion", till exempel dubb. När man här talar om friktion bör det tolkas som skjuvfriktion enligt 6.2.5, där även termen ingår. Denna term bör ses som en del av skjuvfriktionen, inte som något separat bidrag därutöver. En "dubb" med tillräcklig förankring uppåt och nedåt bidrar också till skjuvfriktionen genom sin
area .
Det finns inget i EK2 som anger hur stor del av den totala kraften som behöver kunna tas av dubb eller dylikt. Det blir en bedömningsfråga från fall till fall.
Fråga publicerad 2020-11-26.
Fråga: I 9.2.3 (2) står "Reglerna i 9.2.2 (5) och (6) är i allmänhet tillräckliga för att bestämma erforderlig minimiarmering för vridning". Ska det tolkas som att den minimiarmering som bestäms enligt 9.2.2 för tvärkraft (500 mm2/m) också är tillräcklig för att samtidigt utgöra minimiarmering för vridning? Eller ska man lägga in dubbel minimiarmering enligt 9.2.2 (2 x 500 mm2/m) för att få tillräcklig minimiarmering för tvärkraft och vridning?
Svar: Nej, man behöver inte dubbla armeringen. Syftet med minimiarmering är att undvika grova sprickor och spröda brott, och hänvisningen i 9.2.3 (2) till 9.2.2 (5) är bara ett sätt att ange en lämplig armeringsmängd utan att behöva upprepa vad som står i 9.2.2 (5). Minimiarmering för vridning är aktuell när man inte dimensionerar särskild vridarmering, dvs. när vridmoment inte behöver beaktas för jämvikt i brottgränstillstånd, se 6.3.1 (2).
Fråga publicerad 2020-07-01.
Fråga: En fråga angående 7.3.6 minimiarmering för sprickfördelning och inverkan av vct. Formeln 7.32 utgår ju från fctm. Detta är ju en kapacitet hos betongen vilket borde innebära att de flesta av betongblandningarna som innefattas i hållfasthetsklassen borde överstiga detta tal. Så min fundering är om man egentligen inte borde modifiera siffran för fctm för att täcka in dem värden som överstiger fctm vid framtagande av sprickfördelande armering? Och har vct hos betongen en inverkan på fctm så att man borde modifiera siffran mer för en betong med vct 0,5 än för en betong med vct 0,6?
Svar: Formellt sett är fctm draghållfasthetens medelvärde, vilket innebär att ungefär hälften av alla värden borde vara högre. Ur den synpunkten är det i viss mening (formellt sett) på osäkra sidan att basera minimiarmeringen på fctm, dvs den borde bli otillräcklig i ca hälften av alla fall. Det hela är dock betydligt mer komplicerat än så, och nedanstående förklaring behandlar endast de faktorer som direkt anknyter till frågan.
Draghållfastheten påverkas indirekt av vct genom att den är kopplad till tryckhållfastheten, som i sin tur beror på vct. Någon speciell inverkan därutöver av vct på draghållfastheten är knappast aktuell. Däremot är det viktigt att det hållfasthetsvärde som används svarar mot aktuellt vct, som i vissa fall kan ha föreskrivits ett lågt värde med hänsyn till beständighet, snabb uttorkning eller annat.
Dragspänningen är inte alltid jämnt eller rätlinjigt fördelad i ett tvärsnitt utsatt för tvång av till exempel krympning, vilket innebär att uppsprickning kan ske vid en medelspänning som är lägre än draghållfastheten, dvs att den kraft som fordras för uppsprickning inte alltid behöver motsvara draghållfastheten x dragzonsarean. Detta beaktas med faktorn k.
Rekommenderade värden på k kan dock ge mycket stora armeringsmängder, framförallt i stora tvärsnitt. Det har därför från olika håll, bland annat Sverige, föreslagits begränsningar. I Boverkets EKS har man i konsekvens därmed dragit ner värdena på k, se figur.
Fråga publicerad 2020-07-01.
Fråga: Kan du förklara vad siffror mellan parentes i Figur L.1 (c) betyder, och ska man använda 0.5(1-H/L) istället 0.5 om H<=L?
Svar:

Fråga publicerad 2020-06-30.
Fråga: Vad betyder bokstaven "N" i ett tabellnamn, exempelvis Tabell 4.4N - Minsta täckande betongskikt? Jag har förstått det som att uppgifterna är rekommendationer och inte krav. Stämmer det?
Svar: Bokstaven "N" i ekvationer, tabeller och figurer betyder att ekvationen, tabellen eller figuren är nationellt valbar. Exempelvis tabell 4.4N och de regler som hör till denna ersätts i Sverige med en helt annan tabell och helt andra regler, som ges i Boverkets EKS och Transportstyrelsens TSFS. Huruvida ett nationellt val är råd eller krav beror på hur det är formulerat i EKS och TSFS, det är alltså inte upp till användaren att avgöra.
Fråga publicerad 2020-06-30.
Fråga: I fråga/svar gällande sprickvidd och bestämning av sprickbredd publicerat 2019-09-05 står det: "I ekvation (7.7N) bör f.ö. faktorn k1= 0,8 ingå i täljaren, annars blir det motsvarande fel i omräkningen". I tabellen anges förutsättningarna fct,eff = 2,9 MPa och hcr = 0,5h samt h-d = 0,1 h. Stoppar man in dessa värden i Ekvation 7.7N tycker jag man borde få att uttrycket (fct,eff/2,9) x hcr x k1/(8(h-d)=1,0 eftersom det är dessa värden tabellen utgår från. Men om man räknar ut det får man (2,9/2,9) x 0,5h x 0,8/(8(0,1h) = 0,5 Vad betyder detta? Kan man använda ekvationen ändå eller blir det fel någonstans?
Svar: Ekv (7.7N) gäller vid dragning (centrisk normalkraft), och då är hcr = h den dragna zonens höjd omedelbart före uppsprickning. Med k1 = 0,8 i täljaren blir då resultatet i frågeställarens uträkning = 1,0 som sig bör. Utan k1 skulle det bli 1,25, vilket vore fel.
Fråga publicerad 2020-06-25.
Fråga: I avsnitt 7.2.1.7 hänvisas till "European Technical Product Specification" för att bestämma ccr,sp, scr,sp och hmin. Vilken produktspecifikation menas om jag ska använda vanlig bult med bricka och mutter? Hur kan jag bestämma parametrarna ovan?
Svar: European Technical Product Specification är normalt en ETA (European Technical Assessment) som tillverkaren publicerar, och som är skriven att ett certifierat provningsinstitut avseende en specifik produkt (eller grupp av produkter) från just den tillverkaren. En ETA brukar kunna hittas genom sökning på nätet.
I det aktuella fallet bör produktspecifikationen innehålla de uppgifter om kantavstånd och inbördes avstånd som kan behövas. För en vanlig bult med bricka, där sådana uppgifter saknas, kan man tillämpa 7.2.1.7 (2) b) 2), eller Ekv (7.23). Alternativt kan man kanske jämföra med typgodkända värden för någon speciell produkt med liknande geometri som den aktuella bulten och brickan.
Fråga publicerad 2020-06-25.
Fråga: Tidigare kunde man använda sig av deplacementshöjd (A.5 i SS-EN 1991-1-4) för att kontrollera hur vindlasten påverkas av intilliggande byggnader. Sedan EKS 10 är detta inte tillåtet utan man måste använda sig av vindtunnelförsök (vilket är mycket, mycket kostsamt). Finns det något annat sätt att till exempel se hur vindlasten minskar för varje linje med pelare och balk-stomme i betong under montageskedet?
Svar: Metoden i A.5 har inte tillåtits sedan EKS 8, så det är ingen ändring som skett i EKS 10. Däremot ändras rådet i EKS 11. Tillämpningen av denna författning ger möjligt att även använda sig av numeriska beräkningar.
Den så kallade deplacementshöjden avser dock tätt placerade byggnader och inte pelarrader och balkar eller takstolar i en stomme under uppförandet. Det är däremot tillåtet att reducera vindlasten med hänsyn till under vilken eller vilka månader stommen behöver stagas temporärt under uppförandet.
Det finns det ingen "enkel" modell för att ta hänsyn till en eventuell reduktion av vindlasten med hänsyn till flera pelarrader. Har också svårt att se hur en eventuell reduktion kan säkerställas i och med att vinden ska antas blåsa från godtycklig riktning, och att varje pelarrad under ett montageskede därmed kan komma att utgöra den första pelarraden i förhållande till hur vinden blåser.
Fråga publicerad 2020-06-23.
Fråga: Jag har ett par frågor vid tvärkraftsarmering med mötande C-byglar. 1. Måste tvärkraftsbyglar omsluta alla lager med böjarmering? Eller räcker det till exempel med att två inre lager av tre omsluts? Se SS-EN 1992-1-1 9.2.2 (2) och SS-EN 1992-2 9.2.2 (101). 2. Ska man räkna med skarvlängd eller förankringslängd för mötande de C-byglarna? Om man räknar med förankringslängd, ska man då sätta a=0 mm enligt Figur 8.3 a) om byglarnas skänklar kan förutsättas ligga direkt mot varandra?
Svar: 1. Tvärkraftsbyglar ska omsluta alla lager längsarmering som behövs för att ta den sammanlagda kraften av böjmoment och tvärkraft i aktuellt snitt. Detta är en förutsättning för fackverksanalogin. Om tre lager behövs för denna kraft räcker det således inte att omsluta två lager.
2. För mötande C-byglar gäller skarvlängd. Måttet a i figur 8.3 a) avser det fria avståndet mellan förankrade stänger eller mellan skarvar. Det är inte samma som det (eventuella) fria avståndet mellan stänger i en skarv som visas i figur 8.7. Där finns f.ö.även måttet a definierat för skarvar som ligger i samma snitt, eller som inte kan anses förskjutna.
Beräknad skarvlängd gäller om de skarvade stängerna ligger högst 4Ø eller 50 mm ifrån varandra, annars ska skarvlängden ökas. Måttet i figur 8.3a) påverkar förankrings- och skarvlängden via faktorn α2, och ska enligt figur 8.7 vara minst 2Ø eller 20 mm i en skarv.
Fråga publicerad 2020-06-22.
Fråga: I svenska betongföreningens handbok till SS-EN 1992, Volym 2, kapitel K.3.3.1 nämns att utmattningsbrott i givet tvärsnitt, enligt erfarenhet, aldrig sker i betongen och att eurokod därmed kan ge mycket konservativa resultat. Handboken beskriver att modell enligt BBK 04 kan användas enligt EKS (2009-16). Är samma metod även lämplig för vägbroar tillsammans med TSFS 2018:57?
Svar: Metoden är angiven i Boverkets EKS, men nämns inte i TSFS 2018:57. Det betyder att metoden inte kan tillämpas för broar. Det är lite märkligt, eftersom metoden infördes i BBK 04 med stöd av dåvarande Vägverket. Anledningen var att man hade svårt att räkna hem befintliga broar med avseende på tryckutmattning i betong, om man utgick från variation i tryckspänningar. Tryckutmattning i betong vid böjning är något som enligt försök endast inträffar i överarmerade tvärsnitt; i normalarmerade tvärsnitt är det alltid armeringen som utmattas först. Metoden i BBK 04 löste detta och hade också stöd i forskning.
Fråga publicerad 2019-10-11
Fråga: Inom avsnitt 6.2.3 (7) står det att tillkommande dragkraft i längsarmering på grund av tvärkraft kan beräknas ur redovisad formel. Under formeln står det att den kraften man får ut från momentet/z + delta Ftd inte bör ges större värde än Med.max/z.
För en balk där z varierar i balkens längdriktning på grund av avkortad armering i flera lager, vilket z skall användas för att få fram max-värdet?Vad grundar sig denna begränsning på?Om kombinationen av tvärkraftstillägg+kraft från moment blir större än Med.max/z, skall kraften då sättas till Med.max/z, eller betyder det att förutsättningarna skall förändras för att motverka att detta sker...exempelvis genom justering av trycksträvans lutning?
Följdfråga:
Enligt svaret motiveras begränsningen med att tvärkraften är 0 där momentet är som högst. Hur bör man då tänka i de fall där en balk utsätts för både en utbredd last samt punktlaster...I dessa fall kan en teckenändring ske precis över en punktlast som resulterar i en hög tvärkraft där momentet är som högst. Blir Ftd.max i detta fall (Mmax/z) + (delta Ftd precis i den punkten)?
Se bilder för illustration.
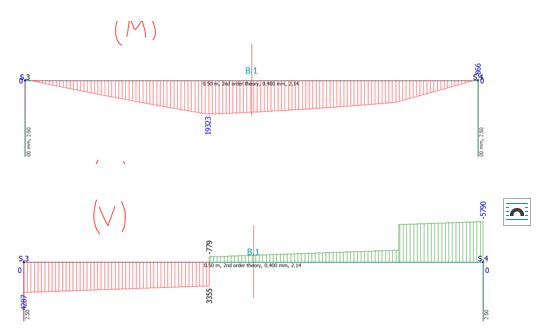
Svar: Man bör använda det z som gäller där maximalt moment uppträder.
Begränsningen grundar sig på att dragkraften inte kan bli större än den som gäller för maximalt moment, där tvärkraften = 0.
När man närmar sig snitt för maximalt moment övergår sprickorna till rena böjsprickor (dvs de blir vertikala i en horisontell balk). Trycksträvornas lutning cot θ då mot noll, och därmed även tvärkraftens inverkan. Om man vill kan man i fackverksmodellen för tvärkraft beräkna hur lutningen minskar, genom att begränsa tvärkraftens inverkan så att den sammanlagda inverkan aldrig blir större än Mmax/z, se illustration nedan.

Kompletterande svar:
Dragkraften kan aldrig bli större än Mmax/z. Det inses kanske lättast om man tittar på ett enklare exempel, en balk med punktlast på mitten, se figur nedan. Inom det område där dragkraften är konstant = Mmax/z minskar trycksträvornas (sprickornas) lutning, och därmed dragkraftstillskottet p.g.a. tvärkraft, mot noll i snittet för maximalt moment.

Fråga publicerad 2019-09-05.
Fråga: Har gått igenom era frågor och svar för tolkning av eurokoden angående dimensionering med avseende på sprickvidd och sprickbreddsbestämning (kapitel 7.3) och har några funderingar.
Vid sprickbreddsbegränsning utan direkt beräkning (7.3.3):
Här är instruktionen att den ena eller den andra tabellen kan användas för att få ut värden, men kan tabellerna 7.2N och 7.3N kombineras? Dvs kan Tabell 7.2N användas för att välja en ø(och därmed armeringsspänning) utefter sprickviddskravet för att sedan sättas in i, den av tabell 7.2N, givna spänningen i tabell 7.3N för att få ut rätt stång avstånd? (Har noterat att kommentarerna ovan tabellerna anger 7.2N för tvång (krympning) samt båda tabellerna för huvudsaklig last, så om inte för krympning så för andra lasttillfällen).
Vid beräkning av sprickbredd vid förhindrad krympning (7.3.4):
Här har vi följt de förslag ni ger i de bifogade svaren för tolkning av euorokoden "För att beräkna en armeringsspänning att sätta in i ekvation 7.1 skulle man då kunna använda ekvation 7.9 och 7.11 "baklänges" utifrån ett visst sprickbreddskrav" samt "Om det gäller att beräkna sprickbredd på grund av förhindrad krympning kan man istället använda en metod som föreslås i svenska betongföreningens handbok till Eurokod 2 (Betongrapport 15), sid 1-98".
Vi kan dock inte se att krypning beaktas någonstans i dessa formler. Vi undrar nu därför om man får beakta krypning i Ekvation 7.9 samt i motsvarande ekvation på sid 1–98 i Betongrapport 15 genom att sätta in Ekvation 7.20 i stället för Ecm när αe räknas ut?
Tilläggsfråga: I svaret på fråga två (näst sista stycket) står det: "Den metod för beräkning av sprickbredd p.g.a. förhindrad krympning, som föreslås i Betongföreningens handbok, har visat sig kunna ge för liten beräknad sprickbredd i stora tvärsnitt, och metoden bör därför inte användas i sådana tvärsnitt." Vad är att betrakta som stora tvärsnitt? Dvs var går gränsen?
Svar: Svaret på den första frågan är att man för sprickor av tvång i första hand bör använda tabell 7.2N. Tabell 7.3N kommer då aldrig in i bilden. För sprickor huvudsakligen orsakade av last kan man använda antingen 7.2N eller 7.3N, men man ska inte använda båda.
I det aktuella sammanhanget handlar det om att bestämma erforderlig armering för sprickfördelning och eventuellt sprickbreddskrav. Om det bara gäller sprickfördelning kan man använda fyk i ekvation (7.1). Om det dessutom finns krav på sprickbreddsbegränsning till ett visst värde kan man behöva använda en lägre armeringsspänning. Man kan då använda tabell 7.2N för vald armeringsdimension och aktuell sprickbredd och avläsa motsvarande armeringsspänning (exempelvis ф 12 och sprickbredd 0,3 mm ger 280 MPa).
Om förutsättningarna avviker från de som står under tabellen bör man dessutom gå in i tabellen med en justerad stångdiameter, dvs ØS bestämd "baklänges" ur ekv (7.7N) i förhållande till vald dimension Øs . I ekvation (7.7N) bör f.ö. faktorn k1= 0,8 ingå i täljaren, annars blir det motsvarande fel i omräkningen.
Svaret på frågan om ekv (7.9) är att krypning inte ska ingå här. Långtids- eller korttidslast beaktas genom faktorn kt. Den citerade ekv (7.20) avser beräkning av deformationer.
Frågor till Helpdesk har kommit in under en lång tidsperiod, och när det gäller just minimiarmering och sprickbredder har det under denna tid varit en del studier och mycket diskussioner i EK2-kretsar. Det förklarar varför svar från olika tidpunkter kanske kan se lite olika ut, utan att vara direkt motstridande.
Att använda en effektiv betongarea i ekv (7.1) var t.ex. en tanke som prövades i ett skede, och som lades fram i ett svar till Helpdesk. Studier visade dock senare att en effektiv area baserad på t.ex. figur 7.1 kunde ge för lite minimiarmering. Därför rekommenderades i ett senare svar till Helpdesk att man tillsvidare skulle använda hela betongarean, med de reduktioner som medges i EK2. Sedermera tillkom i Sverige en regel i EKS 10 som medgav en kraftigare reduktion av denna area; detta kan sägas vara ett steg mot användande av en effektiv area, om än inte samma som enligt figur 7.1.
Den metod för beräkning av sprickbredd p.g.a. förhindrad krympning, som föreslås i Betongföreningens handbok, har visat sig kunna ge för liten beräknad sprickbredd i stora tvärsnitt, och metoden bör därför inte användas i sådana tvärsnitt. Den undre gränsen ska f.ö. skrivas 0,6Ɛcs och inte 0,6σs /Es som det står i utdraget ovan; detta är ett fel som är rättat i utgåva 2 av handboken. Denna undre gräns blir alltid avgörande.
Det kan tilläggas att sprickbredd p.g.a. tvång behandlas även i EN 1992-3 för olika fall och beroende på graden av tvång. Vägledning ges i annexen L och M. I den reviderade Eurokoden kommer detta tema att behandlas i huvuddelen 1-1.
Svar på tilläggsfråga: Det är svårt att ange någon exakt gräns, kanske 300 mm och uppåt.
Fråga publicerad 2019-08-26.
Fråga: Jag har en fråga som gäller andra ordningens moment vid dimensionering av betongpelare. Ska man utgå från minexcentriciteten 20 mm enligt avsnitt 6.1(4) när man räknar fram andra ordningens moment? Eller ska man enbart utgå från initiallutningen enligt avsnitt 5.2(7)? Nästa fråga gäller dimensionering av betongpelare som huvudsakligen är belastade med normalkraft och ledat i båda ändar. Är det tillåtet att använda Ekvation 5.28 i 5.8.7.3(1) eller är det Ekvation 5.30 enligt 5.8.7.3(4) som gäller?
Svar: Minimiexcentriciteten enligt avsnitt 6.1 (4) ska inte vara med vid beräkning av andra ordningens moment, dvs ska inte ingå i första ordningens moment. Det är bara ett minsta värde på den excentricitet eller motsvarande moment som bör användas vid dimensionering av tvärsnitt.
Initiallutning enligt avsnitt 5.2 ska däremot ingå i första ordningens moment, utöver eventuella andra bidrag till detta, och påverkar därmed även andra ordningens moment.
Beträffande Ekvation (5.28) och (5.30) så är (5.28) den mer generella formeln. Den får alltid användas, förutsatt att man sätter in ett lämpligt värde på β, för vilket viss vägledning ges i avsnitt 5.8.7.3 (2). Om man är osäker kan man alltid använda β = 1, vilket leder till Ekvation (5.30), som är en förenklad variant av (5.28). Detta ger resultat en aning på osäkra sidan om första ordningens moment är konstant, men annars ger det i de flesta fall ett resultat som är rimligt eller på säkra sidan.
Fråga publicerad 2019-08-26.
Fråga: Kan vidhäftande spännarmering tillgodoräknas som miniarmering As,min beräknad enligt ekvation (9.1N)? Se nedanstående resonemang som återfinns i en konstruktionsberäkning. "För huvudbalkar: As,min = 2574 x 1,638 = 4216 mm2/m (enligt SS-EN 1992-1-1, avsnitt 9.2.1.1) Då huvudbalkarna är spännarmerade och armeringsmängden enligt SS-EN 1992-1-1, avsnitt 9.2.1.1, avser armering för att få ett segt brott i konstruktionen tillgodoräknas spännarmering här. Mängden spännarmering per balk är 150 x 19 x 5 = 14250 mm2 Vidare är: fyk,spänn = 1860 MPa (mot fyk = 500 MPa ) för ordinarie armering. As,spänn = 14250 x 1860 / 500 = 53010 mm2/m ≫ 4216 mm2→ Ok!"
Svar: Eftersom frågan kommer från Trafikverket utgår svaret från att det handlar om en bro.
Minimiarmering enligt SS-EN 1991-1-1 avsnitt 9.2.1.1 är till för att möjliggöra ett segt brott, och detta gäller även för broar. För spännarmerade konstruktioner tillkommer emellertid ytterligare krav för att säkerställa segt brott, avsnitt 5.10.1. För broar gäller då SS-EN 1992-2 avsnitt 5.10.1 (106), som hänvisar till 6.1 (109), där det anges alternativa metoder för att uppfylla det generella kravet på segt brott.
Metod a) går ut på att visa att konstruktionen klarar ett visst moment med reducerad spännarmeringsarea. För detaljer se SS-EN 1992-2, avsnitt 6.1 (109) a).
Metod b) innebär i princip att det ska finnas en minimiarmering som klarar sprickmomentet, se 6.1. (109). Uttrycket för denna minimiarmering bygger på samma princip som ekv (9.1N). Förespänd armering kan medräknas här enligt speciella regler; för detaljer se 6.1 (110). Efterspänd armering kan däremot inte tillgodoräknas som minimiarmering; här fordras tillkommande slakarmering om alternativ b) ska tillämpas. Här kan det då i stället vara värt att tillämpa alternativ a).
Metod c) "Överenskommelse med behörig nationell myndighet om lämpligt besiktningsprogram baserat på tillfredsställande underlag" är kanske inte aktuell här.
Publicerad 2019-08-26.
Fråga: Vad gäller egentligen med avseende på konstruktion av platta på mark i ett område där grundkonstruktioner ska utföras radonskyddade? Ska armeringen med avseende på täthet dimensioneras enligt SS-EN 1992-1-1 avsnitt 7.3.2 Minimiarmering med avseende på sprickbredds-begränsning? Eller behöver man bara bry sig om detta krav om grundkonstruktionen ska utföras radonsäkert?
Svar: Huruvida det behövs sprickbreddsbegränsning i en platta på mark, och därmed minimiarmering enligt avsnitt 7.3.2, beror på vad slags byggnad plattan ingår i, exponeringsklass, krav på täthet mot radon m.m.
Om det gäller ett småhus behövs i regel ingen sprickbreddsbegränsning och därmed ingen minimiarmering. Om det finns radon i marken kan kanske sprickbreddsbegränsning behövas, och därmed minimiarmering. SS-EN 1992 har dock inga särskilda regler kring detta (tillåten sprickbredd t.ex.); här måste man söka information på annat håll. Möjligen kan man vägledas av regler kring täthet mot vätskor i SS-EN 1992-3 men gastäthet är ju något annat så det är inte säkert att det är relevant. Boverket kan ha information om radon.
För en platta på mark utomhus, eller kanske för industrigolv, kan sprickbreddsbegränsning behövas med hänsyn till exponeringsklass.
Fråga publicerad 2019-08-26.
Fråga: Under avsnitt 9.4.3(1) skjuvarmering med hänsyn till genomstansning visar Bild b placering av bockade stänger. Bilden tillsammans med texten "För upp- eller nedbockade stänger anordnade enligt Figur 9.10 b) kan en enda rad anses vara tillfyllest." missvisar lite tycker jag. Den nedre bilden visar enligt mig J-järn i flera rader eller hur ska man tolka den bilden?
Svar: Bilden visar mycket riktigt flera rader, närmare bestämt tre, men det är bara ett exempel. Texten säger att det också är tillfyllest med bara en rad. Detta i motsats till vad som gäller för vertikala byglar eller stänger, där det bör vara minst två rader.
Fråga publicerad 2019-08-26.
Fråga
Fråga 1: I vilka fall ska avsnitt 7.3.2 användas? En kollega påpekade att avsnitt 7.3.2 liknar avsnitt 4.5.6 i BBK 04, och 4.5.6 används bara för begränsning av sprickor orsakade av tvång. Ska avsnitt 7.3.2 användas bara där det är tvång, eller i alla områden där sprickbreddsbegränsning fordras och dragspänningar förväntas oavsett typ av last?
Fråga 2: Är det tillräcklig att bara använda avsnitt 7.3.2 för att begränsa sprickbredder vid tvång (som t.ex. gjutning av vägg på bottenplatta) (på samma sätt som 4.5.6 i BBK 04)? Eller måste även själva sprickbredderna beräknas med avsnitt 7.3.4 och kontrolleras mot normkrav?
Fråga 3: Vad är anledningen till att avsnitt 7.3.2 används? Är det annars risk för att dragarmeringen flyter precis då det spricker upp, vilket gör att det kan bli större sprickbredder där än beräkningar enligt avsnitt 7.3.4 ger?
Fråga 4: Vad kontrollerar formel (9.1N) som inte täcks in av D.1.4.1 i Krav Brobyggande
(TDOK 2016:0204)?
Fråga 5: I vilka fall behöver formel (9.1N) användas? Kan den skippas för delar som kommer att förbli tryckta t.ex.?
Svar
Fråga 1: Avsnitt 7.3.2 används, precis som det står, där det finns krav på sprickbreddsbegränsning. Det kan gälla sprickor av tvång, t.ex. förhindrad krympning, eller sprickor av last. Där det inte finns krav på sprickbreddsbegränsning, eller där det inte förekommer dragspänningar, kan man bortse från 7.3.2 och Ekvation (7.1).
Fråga 2: Ekvation (7.1) med σs = fyk ger den minsta area som behövs för att armeringen överhuvudtaget ska kunna begränsa sprickbredder. Om det finns ett visst sprickbreddskrav kan man antingen använda Ekvation (7.1) med en lägre armeringsspänning, t.ex. enligt avsnitt 7.3.3, eller genom beräkning av sprickbredd enligt avsnitt 7.3.4. Det förra är mest lämpat när det gäller sprickor på grund av tvång, det senare mest för sprickor på grund av last. Avsnitt 7.3.3 kan dock användas även i detta fall.
Fråga 3: Precis som frågeställaren skriver, så ska en armering enligt avsnitt 7.3.2 förhindra att armeringen flyter när den första sprickan uppstår. Om armeringen flyter kan den inte ta en större dragkraft, som skulle spräcka betongen någon annanstans. Den första sprickan kan då bli okontrollerat stor.
Fråga 4: När det gäller minimiarmering enligt Ekvation (9.1N), liksom de flesta övriga minimiarmeringarenligt avsnitt 9, handlar det i första hand om att möjliggöra ett segt brott. Ekvation (9.1N) ger således arean för den armering som vid flytning kan ta ett moment lika med sprickmomentet i ett böjt tvärsnitt. Med mindre armering kan ett plötsligt brott inträffa om spricklasten uppnås. Med sådan armering kan denna last fortfarande bäras, om än med stor deformation. Formeln är härledd för ett rektangulärt tvärsnitt med vissa förutsättningar, men fungerar approximativt även för andra böjda tvärsnitt.
Fråga 5: Ekvation (9.1N) är härledd för rent böjmoment, och gäller för balkar och plattor. En konstruktion som inte kommer att få några dragspänningar behöver naturligtvis ingen sådan minimiarmering. Men i så fall handlar det snarare om pelare eller väggar, och dessa har sina egna regler (avsnitt 9.5 och 9.6). För balkar och plattor skulle man kunna tänka sig att reducera minimiarmeringen om det finns en yttre tryckkraft, och det går att härleda uttryck för detta, men för detta lämnas f.n. ingen öppning.
Fråga publicerad 2019-08-26.
Fråga: Jag letar efter information som kan hjälpa mig att redogöra och verifiera hur trapptoppen möter de teoretiska kraven. Tvärkraftsarmering skall dimensioneras i trapptopp. Finns det idag några konkreta riktlinjer för detta specifikt? Vilken standard är högst lämpligast att följa genom en beräkningsgång?
Svar: Några specifika riktlinjer för dimensionering av "trapptoppar" finns inte. Tvärkraftsarmering dimensioneras enligt SS-EN 1992-1-1 (Eurokod 2) avsnitt 6.2.3, men "trapptoppar" (antar att det är hakupplag som avses) inrymmer speciella problem med tanke på små dimensioner och dåligt utrymme för armering täckskikt. Gäller i lika hög grad trappans nedre del samt upplag på trapplanen. Beroende på geometri kan det även bli fråga om att använda fackverksmodeller, i Eurokoden. Aktuella avsnitt i Eurokoden är då 5.6.4 och 6.5.
Fråga publicerad 2019-08-26.
Fråga: Jag har en analysmodell som i grova drag kan liknas vid en fritt upplagd betongbalk. För denna icke-linjära analysmodell så har tryckhållfastheten och draghållfastheten hos betongen reducerats med partialkoefficienter. Vid applicering av last i mitten av "balken", fås ett nästintill läroboksexempel av ett böjbrott. Dock så fås väldigt höga principiella spänningskoncentrationer i överkant och tycks indikera att betongen i tryckzonen är nära att gå till brott. Jag har som sagt enbart reducerat hållfastheten hos betongen och inte E-modulen. Intuitivt anser jag detta ge missvisande resultat (gällande spänningskoncentrationen) då en sprödare konstruktion fås som har större benägenhet för spänningskoncentrationer. Reduktion av även E-modulen skulle i teorin ge större deformationsförmåga i den tryckta betongen och mer jämnt fördelade spänningar över tryckzonens höjd. Jag undrar då hur ska man tänka vid appliceringen av partialkoefficienter för materialen i en icke-linjär FEM analys. Kan man bortse från att använda partialkoefficienterna eller bör man även reducera andra parametrar (för att behålla relationen/korrelationen mellan parametrarna, liknande den verkliga relationen hos exempelvis betongens E-modul och tryckhållfasthet)? Eller bör man förhålla sig till att reducera endast hållfasthet hos materialen som för analytiska beräkningar?
Svar: Det "normala" vid icke linjär analys är att använda ett slags medelvärden på materialparametrar och sedan, om man vill ha ett dimensioneringsvärde för brottgränstillstånd, dividera med en global säkerhetsfaktor. Detta "säkerhetsformat" är närmare beskrivet i SS-EN 1992-2 avsnitt 5.7 och bilaga PP. Säkerhetsformatet vid icke linjär analys diskuteras dock fortfarande, och reglerna härvidlag kan komma att förbättras. Mer ingående behandling av ämnet finns även i fib Model Code 2010.
I avsnitt 5.7 (5) och 5.8.6 (3) i SS-EN 1992-1-1 nämns respektive beskrivs även användning av icke-linjär analys med dimensioneringsvärden, vilket direkt ger ett dimensioneringsvärde för bärförmågan i brottgränstillstånd. Denna metod är f.n. enligt 5.7 (5) nämnd för andra ordningens analys av slanka konstruktioner, men detta kan komma att ändras. Metoden har använts vid kalibrering av de förenklade metoderna för andra ordningens analys i avsnitt 5.8.7 och 5.8.8. I detta fall reduceras även betongens E-modul till ett dimensioneringsvärde, med partialkoefficienten 1,2. Reduktion av betongens E-modul föreskrivs i 5.8.6, men även i SS-EN 1990 står någonstans att styvhetsparametrar kan behöva reduceras vid andra ordningens analyser.
Att enbart reducera hållfastheten och inte E-modulen ger en "orealistisk" arbetskurva, vilket möjligen kan förklara de beskrivna resultaten. Även reduktion av E-modulen med 1,2 och hållfastheten med 1,5 ger en i viss mening orealistisk arbetskurva, om än inte i lika hög grad. Vid andra ordningens analys spelar dock detta ingen roll, eftersom bärförmågan vanligen uppnås innan betongen krossats i den omfattning som beskrivs i frågan.
För övrigt behöver det beskrivna resultatet inte vara orealistiskt. Även i en balk som inte är överarmerad kommer betongen så småningom att få höga töjningskoncentrationer i överkanten, om pålastningen drivs vidare efter det att armeringen börjat flyta. Det hela beror även på hur lasten är modellerad. En "punktlast" med liten eller ingen utbredning måste ofrånkomligen ge orealistiska spännings/töjningskoncentrationer.
Fråga publicerad 2019-04-05.
Fråga: Har en fråga angående SS-EN 1992-1-1, kap 8.9.1 (4). Två stänger ovanför varandra betraktas inte som en bunt. Vi undrar dels hur det tillgodoses att "goda vidhäftningsförhållande föreligger", dels hur sprickbredder för denna utformning av armering beräknas? Vilken av Aef, As respektive φ som används vid beräkningar, där
1) Aef är effektiv betongarea för den del av dragzonen som har samma tyngdpunkt som den vidhäftande armeringen
2) och där As är area för direkt vidhäftande dragarmering. Beräknas här stångens area två gånger?
3) samt hur beräknas φ som är stångdiameter?
Svar: Vad som är" goda vidhäftningsförhållanden" respektive inte definieras i kap 8.4.2 (2), och bör kunna tillämpas även här.
När det gäller parametrar i sprickbreddsberäkningar ges ingen vägledning för detta speciella fall i SS-EN 1992. Här är ett förslag till svar på de konkreta frågorna:
1) För Aef fungerar den vanliga definitionen oavsett om stängerna betraktas som bunt eller inte. Armeringens tyngdpunkt är väl definierad.
2) As bör vara arean för de två stängerna.
3) För att regeln i 8.9.1 (4) ska ha någon mening bör man här kunna använda φ som stångdiameter; att använda roten ur φ skulle ju innebära att stängerna betraktas som en bunt. För 2φ finns inget motiv.
Fråga publicerad 2019-04-04.
Fråga: I SS-EN 1992-1-1, 6.1(4) står:
(4) För tvärsnitt med symmetrisk armering belastade med tryckkraft förutsätts en minstra excentricitet e0 = h/30, dock minst 20 mm (h är tvärsnittets höjd).
Jag har tolkat detta som minsta excentricitet som man skall använda vid beräkningen inte tilläggsexcentricitet, när lastens excentricitet överstiger emin då räknas endast med lastens excentricitet, exempel:
emin=max(h/30, 20mm)
e0=Med/Ned ≥ emin
Anser ni tolkningen vara rätt?
Svar: Tolkningen är korrekt, emin används bara som en mista excentricitet vid tvärsnittsdimensionering och ska inte adderas till excentricitet enligt strukturanalys.
Fråga publicerad 2019-03-11.
Fråga: I kap 9.6.2 står det att för en vägg ska den vertikala armeringen minst vara As,vmin0,002Ac, där står det under (2) att "Om minimiarmeringen, As,vmin, är dimensionerande bör armeringen fördelas jämt mellan de två väggytorna, dvs 0,001 Ac / yta. I kap 9.6.3 står att horisontell armering bör läggas in i alla ytor. Den bör inte understiga As,hmin, som är 25% av den vertikala armeringen eller 0,001 Ac. Här står det dock inte att hurvida den ska fördelas jämt mellan de två ytorna. Hur ska man tolka rekommendationen för den horisontella minimiarmeringen. Ska det vara 25% resp 0,001 Ac per väggyta, eller totalt i väggen som ska fördelas på två ytor?
Svar: För vertikal armering betecknar As,vmin helt klart den totala arean för minimiarmering. För horisontell armering är det inte lika tydligt. Här kan beteckningen As,hmin möjligen uppfattas som gällande för vardera ytan. Även denna beteckning bör dock uppfattas som gällande för den totala arean, som sedan fördelas lika mellan båda ytorna.
Fråga publicerad 2019-03-11.
Fråga: För förspända balkar pratas det om dimensionering och kontroll av fenomenen Spjälkning och Klyvning (Splitting & Spalling) i balkens ändar. Jag hittar ingen direkt referens till dessa fenomen i SS-EN 1992. Finns det några riktlinjer för en sådan beräkning som då officiellt kan sägas vara "enligt norm"?
Svar: Det finns ingen speciell vägledning för dimensionering m.h.t. spjälkning och klyvning i samband med förankring av spännarmering.
Båda fenomenen handlar om koncentrerade krafter i s.k. diskontinuitetsområden. Den lilla vägledning man kan hitta är dels det som gäller allmänt för analys med fackverksmodeller i 5.6.4, dimensionering med fackverksmodeller i 6.5 samt lokalt tryck i 6.7 (aktuellt framförallt vid förankring av efterspänd armering). Vidare står lite om förankringszoner för efterspänd armering i 8.10.3, bl.a. med hänvisning till 2.4.2.2 (3) beträffande en speciell partialkoefficient för spännkraft i detta sammanhang, vilket är viktigt.
I övrigt kan hänvisas till MC 2010, där det ges en del vägledning bl.a. när det gäller förespänd armering, vilket blir lite annorlunda jämfört med efterspänd.
Fråga publicerad: 2018-11-19
Fråga:För förspända balkar pratas det om dimensionering och kontroll av fenomenen Spjälkning och Klyvning (Splitting & Spalling) i balkens ändar. Jag hittar ingen direkt referens till dessa fenomen i EC2. Finns det några riktlinjer för en sådan beräkning som då officiellt kan sägas vara "enligt norm"?
Svar:Det finns ingen speciell vägledning för dimensionering m.h.t. spjälkning och klyvning i samband med förankring av spännarmering.
Båda fenomenen handlar om koncentrerade krafter i s.k. diskontinuitetsområden. Den lilla vägledning man kan hitta är dels det som gäller allmänt för analys med fackverksmodeller i 5.6.4, dimensionering med fackverksmodeller i 6.5 samt lokalt tryck i 6.7 (aktuellt framförallt vid förankring av efterspänd armering). Vidare står lite om förankringszoner för efterspänd armering i 8.10.3, bl.a. med hänvisning till 2.4.2.2 (3) beträffande en speciell partialkoefficient för spännkraft i detta sammanhang, vilket är viktigt.
I övrigt kan hänvisas till MC 2010, där det ges en del vägledning bl.a. när det gäller förespänd armering, vilket blir lite annorlunda jämfört med efterspänd.
Avsnitt i eurokoden: 8.9.1 (4)
Fråga publicerad: 2018-11-14
Fråga: Två stänger ovanför varandra betraktas inte som bunt.Vi undrar dels hur det tillgodoses att "goda vidhäftningsförhållanden föreligger", dels hur sprickbredder för denna utformning av armering beräknas.Vi undrar vilken Aef, As resp f som används vid beräkningar, där:
Svar: Vad som är "goda vidhäftningsförhållanden" respektive inte definieras i 8.4.2 (2), och bör kunna tillämpas även här. När det gäller parametrar i sprickbreddsberäkningar ges ingen vägledning för detta speciella fall i EK2. Här är ett förslag till svar på de konkreta frågorna:
Fråga: När jag läser in eurokoderna stöter jag på problem. Det framgår inte tydligt att tabell 4.3N & 4.4N (där bärverksklasserna S1 – S7 styr beroende på exponeringsklass täckskiktet) inte skall användas och ersättas med tabell 4.4S. Det anges därmed inte tydligt och dessutom finns det inte någon notering att Tabell 4.5N är inkluderad i denna ersättning. Jag hittar inte någonstans vad de olika Bärverksklasserna S1 – S7 betecknar, d.v.s. en beskrivning av dem. Även om de inte skall användas så vill jag veta vad de betyder. Det kan vara viktigt för de fall då man skall bedöma anbud där Bärverksklasser används.
Det var först när jag läste i Svenska Betongföreningens handbok till Eurokod 2 som det framgår att:
”Det betyder även att de s.k. bärverksklasserna i tabell 4.3N – 4.5 inte alls kommer till användning i Sverige.” (Sid 1-25)
Denna förklarande upplysning hittar jag inte i EKS 6 och Nationella anpassningsbilagan (NA).
1. Var finns beskrivningen av Barverksklasserna?
2. Varfor finns det inte enkelt noterat i (NA)?
Svar: Det framgår av standarden att det finns ett nationellt val. Då måste man läsa i Boverkets/Trafikverkets föreskrift och se vilket det nationella valet är.
Frågeställningen missar en avgörande detalj som svarar på nästan alla ställda frågor, nämligen att EKS är överordnad eurokod. Regler i EKS ska anses ersätta, modifiera, komplettera eller begränsa motsvarande regler i eurokod beroende på sammanhanget. Detta behöver inte upprepas vid varje punkt där nationellt val (NDP) kan göras. I alla dessa fall ska reglerna i EKS alltid gälla gentemot motsvarande regler i eurokod.
Val av täckskikt enligt 4.4.1.2 (5) är i eurokod baserad på val av bärverksklass. Anmärkningen i samma avsnitt anger att värdena på (som är huvudmålet för avsnitt 4.4.1.2 (5)) kan väljas nationellt. I EKS anges dessa värden i tabell 4.4(S), som ersätter tabell 4.3N till 4.5N, men här baseras valet på en modell som inte är beroende av några bärverksklasser. Och eftersom bärverksklasserna enbart används vid val av , om man använder sig av eurokodsmodellen, så blir hela konceptet om bärverksklasserna ointressant i Sverige.
Fråga: Vad gäller utförande och kontroll när det kommer till betong?
Vilka utförandeklasser/tillverkningsklasser finns?
Vilka standarder tar upp detta? Är det samlat i en standard som t.ex. SS-EN 13670?
Svar: Eurokoder för stål och betong behandlar inte utförande och kontroll, men hänvisar till andra EN-standarder för det. För utförande av betongkonstruktioner hänvisar SS-EN 1992-1-1 (SS-EN 1992-1-1) till SS-EN 13670? och i den ges det utförandeklasser. När det gäller tillverkning av betong hänvisar SS-EN 1992-1-1 till EN 206. I SS-EN 206 behandlas fordringar, egenskaper, tillverkning och överensstämmelse för betong. Tillämpning av SS-EN 206 i Sverige beskrivs i standarden SS 137003, där även kopplingen till våra tidigare tillverkningsklasser behandlas i viss mån.
Reglerna i eurokoden och andra relevanta europeiska standarder är inte riktigt kompatibla med våra gamla regler i BBK när det gäller utförandeklasser/tillverkningsklasser. Det pågår nu ett arbete för att inkorporera vad som behövs av våra gamla regler i EKS, men det kommer att dröja ett tag innan den här ändringen slutligen skulle träda i kraft. Tills dess bör man tillämpa SS-EN 13670 och SS-EN 206 med tillhörande regler i EKS, se kap. 2.1.1.
Fråga: SS-EN 1992-1-1. Den mest akuta frågan för oss är angående beräkning av kryptalet enligt kapitel 3.1.4. I detta kapitel finns diagram som kan användas för framtagande av kryptalet ett för RH 50% och ett för RH 80%. Vi föredrar att beräkna kryptalet enligt en formel, så att vi kan använda beräkningsprogram som MathCad och Excel. Då hänvisas vi till Appendix B. Det vi konstaterar när vi kontrollerar våra beräkningar är att diagrammen och formeln ger mycket stora skillnader i resultatet. Differensen är så stor att man kan anta att antingen diagrammen eller formeln är felaktig. Vilken metod är det tänkt ska användas och är denna metod diagramvarianten, hur är det tänkt att dessa ska implementeras i databeräkningar?
Svar: Tanken är att man kan använda figur 3.1 när man bara behöver slutvärdet på kryptalet och när förutsättningarna stämmer hyggligt med diagrammens förutsättningar. Bilaga B kan användas när man behöver tidsförloppet och/eller behöver ta hänsyn till fler parametrar. Ytterligare en anledning att använda bilaga B är ju att man vill beräkna kryptalet i ett program. Jag har själv använt bilaga B många gånger, men inte gjort direkta jämförelser med figur 3.1.
Fråga: SS-EN 1992-1-1. Förankring av längsgående stänger. Tabell 8.2 hänvisar till figur 8,1 (b), (c) och (d). I Figur 8,1 förekommer figurbenämningen b) på 3 ställen, c) och d) saknas. Är det så att de tre sista figurerna skall vara i tur och ordning c), d) och e)?
Svar: De tre sista figurerna ska mycket riktigt vara c), d) och e). Felet finns bara i den svenska översättningen, inte i det engelska originalet.
Fråga: Berör SS-EN 1992-1-1.
Gäller punkt (3) både brott- och bruksgränstillståndet? Kan temperaturen aldrig vara huvudlast?
Svar: Punkt (3) gäller i båda fallen. Det ska inte tolkas som att temperaturlast inte kan vara huvudlast. Om man räknar med temperatur, så är den en variabel last på vilken man ska använda partialkoefficienter enligt den lastkombination som gäller för respektive gränstillstånd enligt SS-EN 1990 och SS-EN 1991-1-5. D.v.s. också som huvudlast (som i bruksgränstillståndets frekventa och kvasipermanenta kombinationer även innehåller ψ-faktorer). Huruvida man i brottgränstillstånd ska räkna med temperaturlast i betongkonstruktioner bestäms av SS-EN 1992-1-1, 2.3.1.2 (2).
Fråga: SS-EN 1992-1-1. Enligt minimiarmering enligt Eurokod SS-EN 1992-1-1:2005 kap 7.3.2
Ac1 = betongytan inom den dragna zonen.
Vid tjocka plattor som t.ex. skyltfundament och liknande blir det orimligt mycket minimiarmering. Kan värdet på Ac1 begränsas likt Ac, eff enligt figur 7.1?
Svar: SS-EN 1992-7-3-2 kan ge mycket minimiarmering i tjocka konstruktioner, beroende på att armeringen ska relateras till betongarean Ac1 = den totala dragzonen före uppsprickning. I ett fall med rent dragtvång (t.ex. förhindrad krympning) innebär det att minimiarmeringen relateras till hela betongarean. Detta ger då betydligt mer armering än enligt motsvarande regel i BBK, där armeringen relateras till en effektiv area närmast kring armeringen, som kan vara betydligt mindre, speciellt i tjocka tvärsnitt. I SS-EN 1992 kan man visserligen reducera minimiarmeringen med en faktor k; som är 1,0 för tvärsnitt med upp till 300 mm höjd och sedan minskar linjärt till 0,65 för höjd 800 mm eller mer. Detta kommer ändå att ge betydligt mer armering än BBK vid ren dragning.
Vid böjning kan man reducera med ytterligare en faktor kc som blir 0,4 vid ren böjning i ett rektangulärt tvärsnitt, och eftersom dragzonen före uppsprickning då endast omfattar halva tvärsnittet blir den totala reduktionen 0,2. Det är således framförallt vid ren dragning som minimiarmeringen kan bli kraftig.
Formuleringen ”vid krav på sprickbreddsbegränsning” innebär att det inte behövs någon minimiarmering där sådant krav inte föreligger. För en tjock platta behöver man inte alltid ställa sådana krav när det gäller plattans inre, utan ofta endast vid kanterna där armeringen finns. I så fall bör det vara tillfyllest att endast minimiarmera områdena närmast kring armeringen. Den effektiva betongarea Ac, eff som används vid sprickbreddsberäkning enligt 7.3.4 är något större än motsvarande enligt BBK, och borde därför kunna användas som grund för minimiarmering enligt detta resonemang. I så fall bör man dock självklart sätta k = kc=1
Ett sätt att styra mot mindre sprickbredd kan vara att i ekvation (7.1) sätta in en armeringsspänning enligt tabell (7.3N). Man bör då vara medveten om att tabellerna 7.2N ooch 7.3N kan ge mycket konservativa resultat vid jämförelse med en sprickbreddsberäkning, och därmed troligen även i detta sammanhang.
Icke linjära FE-analyser som gjorts av Mikael Hallgren tyder på att armering enbart vid kanterna kan ge god sprickfördelning inom en viss ”effektiv betongarea”, även om sprickorna i den oarmerade inre delen av tvärsnittet kan vara få och grova. Detta ger visst stöd för resonemanget ovan.
I Trafikverkets förslag till ändringar i VVFS 2004:43 finns en skrivning som förtydligar det som du undrar.
Fråga: En fråga om SS 137003:2008 (Sv), kapitel 5.5.3, fotnot Anm: Var hittar jag de kompletterande kraven? Alltså vad gäller för vattentät betong, ensidigt vattentryck och inläckage godtas ej?
Svar: Kompletterande krav kan t.ex. bestå av krav på maximal sprickbredd. Någon regel som wk, max= 0,20 mm för rimligt vattentäta konstruktioner enligt BBK04 finns inte i SS-EN 1992 allmän del (SS EN 1992-1-1), men det finns i specialdelen som behandlar ”Behållare och avskiljande konstruktioner för vätskor och granulära material” (SS EN 1992-3). Frågan är egentligen inte någon fråga om text i eurokoderna och bör egentligen ställas till den tekniska kommitté som tagit fram den svenska standarden SS 137003, vilket är SIS/TK 190.
Enligt SS-EN 1992-3, 7.3.1 kan man ange krav på täthet med hjälp av fyra täthetsklasser, från i princip grundkraven enligt SS-EN 1992-1-1, 7.3.1 (klass 0) till att inget läckage alls accepteras (klass 3). Kraven och verifieringen av dem är olika i de olika klasserna. Det är enbart i klass 0 och 1 som sprickvidd är kriteriet. SS-EN 1992-3 är dock fortfarande inte införlivad i det svenska regelsystemet (genom Boverkets EKS och Trafikverkets EBS). Man får, alltså, endast använda denna eurokod som en ”extern” handbok/beräkningsmodell.
Trots att SS-EN 1992-3 ännu inte är formellt införd hänvisar Trafikverkets TK Bro till täthetsklass 2 enligt denna standard (med rekommenderade värden) för konstruktioner utsatta för ensidigt vattentryck.
Kommentar: SIS/TK190 har medverkat i svaret.
Fråga: Frågan gäller tvärledsarmering vid omlottskarvning av armering enligt 8.7.4.1 Enligt (2) erfordras ingen tvärarmering för skarv av järn upp till ø 20. Enligt (3) erfordras tvärarmering för skarv av järn över ø 20 samt (3) andra stycket: om mer än 50% skarvas ska tvärarmeringen utgöras av byglar. Tolkningen är huruvida andra stycket i (3) gäller även för (2) (armering under ø 20)? (Jag tycker dock att texten i (2) motsäger detta).
Svar: Andra stycket i (3) gäller endast för ø 20 och uppåt. Om diametern är ø 20 eller större och om mer än 50% är skarvat i samma snitt, så ska det således inte bara finnas tvärarmering, den ska dessutom bockas in i tvärsnittet. För armering med ø < 20 men med mer än 25% skarvat i samma snitt, fordras tvärarmering, men det räcker med vanlig rak tvärarmering, även vid mer än 50%. 29 wk, max.
Fråga: Håller på att upprätta egenkontroller för produktionen på NCC Construction. Jag har stött på problem när det kommer till utförandet av gjutning av betongkonstruktionen. Vad ska jag hänvisa till för regelverk? SS-EN 13670 finns väl inte ute än?
Svar: Frågan är egentligen ingen Eurokodfråga, men utförandestandarden SS-EN 13670 hänvisas det till från EK2, SS-EN 1992-1-1. Den är även införd i BFS 2011:10 - EKS, och SS-EN 13670 gäller i Sverige. Den blev fastställd som svensk standard 2009-12-09. En svensk tillämpningsstandard SS-137006:2011 har också utarbetats.
Fråga: I betongnormen SS-EN 1992-1-1, avsnitt 4.4.1.2(5) nämns begreppet “bärverksklass”. Var kan man hitta definitionen av detta? Jag har letat både i nämnd norm och i SS-EN 1990 utan framgång.
Svar: Bärverksklasserna i det här fallet används endast för val av rekommenderade värden på täckskikt och definieras i avsnitt 4.4.1.2 i SS-EN 1992-1-1 genom tabellerna 4.3N – 4.5N. Samma begrepp används i SS-EN 1991-1- 7 också, men med en helt annan betydelse vid beräkning av olyckslaster. I den svenska tillämpningen av avsnitt 4.4.1.2 i SS-EN 1992 används inte de rekommenderade värdena, utan istället de värden som sedan 2003 funnits i SS 13 70 10 och som tillämpats tillsammans med BBK 04. Det betyder att begreppet bärverksklass inte används i Sverige vid beräkning av min. täckskikt.
Fråga: Kan spänningarna i betongen för en vägbro beräknas på samma sätt som för en järnvägsbro (se SS-EN 1992-2 Bilaga NN 3.2, ekv. NN.113)? Med skillnad att lc sätts lika med 1,0 och σc, 72 ersätts med σc, LM 1.
Svar: För vägbroar innehåller λ –metoden inte verifiering av spänningar i betongen. Dessa måste alltså kontrolleras enligt SS-EN 1992-2, 6.8.7. Det går inte att överföra det som i bilaga NN gäller för järnvägsbroar till vägbroar.
Fråga: En fråga angående dimensionering av utsträckta betongfundament (Pad footings). Oftast väljer man ett fundament som är tillräckligt brett för att fördela grundtrycket gentemot markens bärförmåga. Eftersom fundamentet blir utsträckt behöver man oftast öka höjden för att klara tvärkraft och genomstansning. Ska man tolka SS-EN 1992 så att man kräver minimi armering i fundament med reglerna som gäller för betongplattor generellt? (9.2.11 9.1N) Ett fundament som görs 600 mm tjock kräver i ett hypotetiskt fall, ex. 2500 mm2/m för att klara bärförmåga, sprickbredd, tvärkraft o.s.v. Om man istället väljer att göra fundamentet 800 mm ökar armeringsbehovet till 3500 mm2/m endast med kravet på minimi armering. Räcker det att uppfylla krav på bärförmåga eller måste man strikt följa regeln om minimi armering? Fundament är ju egentligen inte lika känsliga för spröda brott på samma sätt om ett betongbjälklag, och då denna regel kan tyckas onödig och oekonomisk. Om ja, ska man använda reglerna för oarmerade konstruktioner annars? Om ja, kommer fundament i princip alltid att armeras utgående från minimiarmering m.h.t. deras tjocklek?
Svar: Ekvation 9.1N är avsedd för balkar och plattor som kan beräknas med balkteori. Formeln ger egentligen den mängd armering som erfordras för att klara sprickmomentet i ett rektangulärt tvärsnitt. En grundplatta med tjockleken 800 mm har vanligen en geometri där beräkning med balkteori inte gäller längre. Det blir snarare ett fall som liknar en hög balk, men det beror förstås på de övriga måtten i fundamentet. Man måste alltså använda rätt modell med hänsyn till geometrin. Ett slankt fundament kan dimensioneras med balkteori, och då gäller avsnitt 9.1 och avsnitt 9.2. Ett högt/tjockt fundament bör istället dimensioneras med fackverksmodell, och då gäller inte 9.1 och 9.2. I båda fallen bör man dock följa avsnitt 9.8.2 Grundplattor.
Fråga: En fråga beträffande SS-EN 1992-1-1:2004. Vid punkten 7.3.3(5) anges: “Cracking due to tangential action effects may be assumed to be adequately controlled ...”. Min fråga gäller då vad som avses med tangentiella lasteffekter, d.v.s. vad är det för lasteffekter?
Svar: Det som åsyftas är sprickbildning p.g.a. skjuvning, tvärkraft och/eller vridmoment, i motsats till sprickbildning av normalspänningar (böjning, dragkraft).
Fråga: Var finns uppsprickningskritieriet för betong i brottgränstillstånd (ULS)? (motsvarande fanns tidigare i BBK 3.5)
Svar: Eftersom du hänvisar till BBK 3.5 antar jag att det handlar om oarmerad betong. I så fall är det SS-EN 1992 12.3.1 ekvation (12.1) som gäller med = 0,5 enligt svensk NA (eller Boverkets EKS). Detta ger samma utnyttjande av draghållfasthet i brottgränstillstånd som enligt BBK.
Fråga: 1. I SS-EN 1992-2, 5.3.1, sägs att punkt 5.3.1 (2) i SS-EN 1992-1-1 inte gäller. Det anges även att 5.3.1 (6) inte gäller. Detta verkar dock onödigt då 5.3.1 (2) bl.a. behandlar just (6). Frågan är dock när en konstruktion ska anses vara balk, alternativt platta, om inte punkt 5.3.1 (2) är gällande längre. 2. SS-EN 1992-1-1, 6.4: Finns det någon begränsning vad gäller sidoförhållandena för när endast genomstansning kontrolleras? Tänker på pelare med avlångt eller stort tvärsnitt. Tidigare kontrollerades tvärkraft på viss del av tvärsnittet. 3. SS-EN 1992-1-1, 6.4: Tidigare kunde man dimensionera en innerpelare för genomstansning genom att sätta total last till fyra gånger lasten på mest belastade kvadrant, samtidigt som excentricitetsfaktorn sattes till 1.0. Går det fortfarande att göra så?
Svar: Fråga 1: Genom borttagning av 5.3.1(2) i SS-EN 1992-1-1, borttas begränsningen av (3) – (7) till endast byggnader. Det leder till att punkterna (3) till (7) även blir gällande till andra konstruktionstyper (t.ex. broar). Eftersom (6) inte anses gälla vid broar behöver man även ta bort denna punkt. Alltså, för broar gäller punkterna (3), (4), (5) och (7) men inte (6) och det besvarar resten av frågan.
Fråga 2: Nej, någon egentlig begränsning av sidoförhållande som i BBK finns inte. I fallet utan skjuvarmering blir det inget problem eftersom beräkningsformeln för genomstansning enligt (6.47) är samma som för 2D-fallet med enkelspänd skjuvning enligt (6.2). Det kan bli besvärligt om man måste tillsätta skjuvarmering, eftersom stansning då räknas med en additionsmodell, medan enkelspänd skjuvning räknas med fackverksmodell. Här saknas en tydlig anvisning. Men eftersom det inte är motstridigt bör det gå att använda principen enligt BBK eller Betonghandboken-K för att skilja på stansning och skjuvning i fall med t.ex. fria väggslut.
Fråga 3: Nej. Exentricitetsfaktorn ska beräknas enligt 6.4.3. Där finns det dock en förenkling som säger att man kan approximera excentricitetsfaktorn till 1,15 för innepelare, men då får längderna på angränsande spann inte avvika mer än 25 % från varandra.
Fråga: En fråga angående att beräkna böjarmering i fält för en väggskiva. I SS-EN 1992 avsnitt 9.7(3) hänvisas det till en beräkningsmodell, och jag undrar vilken modell det är som åsyftas? Kan man använda sig av beräkningsgången enligt avsnitt 3.1.7. Detta är ju inte tillåtet i den svenska normen, då man enligt BBK ska följa beräkningsgången för avsnitt 6.6.3.3. Skriver examensarbete för ett konsultföretag där min uppgift är att ta fram beräkningar för tvärsnittbetong, pelare, vägg osv. Undrar hur man beräknar hur mycket armering man behöver i drag. Och om man behöver i drag, hur många lager och hur avgörs det? Behöver man i tryck också, och hur avgörs det i sådana fall?
Svar: Beräkningsmodellen för höga balkar bör enligt eurokoden baseras på fackverksmodell. De modeller som beskrivs i 3.1.7 gäller för ordinära balkar, där man kan förutsätta rätlinjig töjningsfördelning, och är således inte tillampliga for höga balkar. Några speciella regler om användning av fackverksmodeller i höga balkar ges inte i SS-EN 1992, annat än för dimensionering av noder och trycksträvor, avsnitt 6.5. Tillsvidare finns alltså ingen motsvarighet till BBK:s detaljerade regler om t.ex. inre hävarmar för höga balkar. Vi arbetar dock på att fylla denna lucka i Svenska Betongföreningens handbok om SS-EN 1992, som bl.a. kommer att ge utförliga anvisningar och beräkningsexempel kring användning av fackverksmodeller, inte minst för höga balkar. Som en enkel tumregel kan tillsvidare sägas att inre hävarmar bör begränsas så att lutningen för huvudtrycksträvorna i fackverket (eller tryckbågens största lutning i modell ”båge med dragband”) inte överstiger ca 70°. Lutningen begränsas naturligtvis även så att tryckbågen respektive trycksträvorna ryms inom tvärsnittet med godtagbar tryckspänning.
Mycket mer än så kan inte sägas på detta begränsade utrymme. Det kan dock tilläggas att fackverksmodell och modell ”båge med dragband” inte är väsensskilda, utan bara olika sätt att uttrycka samma sak. En båge med dragband med inre hävarm enligt BBK kan i regel visas ge ett resultat som skulle vara acceptabelt även enligt eurokoden. Möjligen kan eurokodens regler om noder (6.5.4) ge lite andra resultat än BBK:s regler om bärförmåga vid upplag, men jag kan inte säga hur det ”slår”.
Fråga: Enligt BBK 04 3.9.4 beräknades ”bockningsradie”, men i Eurokod 2 8.3 beräknas ”tillåten dorndiameter”. Har stämt av med en av armeringsleverantörerna, armeringenheten på BE Group, och de önskar fortsättningsvis att bockningsradie anges på armeringsförteckningar (och inte dorndiametern). Jag kan inte hitta någon hänvisning i eurokod om hur jag ska översätta dorndiameter till bockningsradie. Om de standardiserade bockningsradierna med motsvarande dorndiameter i BBK fortfarande gäller, undrar jag om det finns någon hänvisning dit? Eller finns någon tabell i eurokod motsvarande tabell 3.9.4.2a i BBK 04?
Svar: Det räcker med att svara att en sådan tabell inte finns i det nya eurokodsystemet. Tabell 3.9.4.2a i BBK 04 ger en ungefärlig relation mellan dorndiametern till resulterande bockningsdiametern. För att få en exakt relation måste man prova sig fram vid varje tillfälle. Hur mycket en elastisk ”återbockning” blir efter bockningen beror självklart på andra parametrar än bara dorndiametern, t.ex. temperatur, materialegenskaper etc. Men man kan fortfarande använda Tabell 3.9.4.2a i BBK 04 som ledtråd om man vill.
Frågan är inte så enkel som det kan verka vid första påseende (förutom att radie = diameter/2). Man måste här skilja mellan minsta bockningsradie m.h.t.
a) risken för skador på armeringen och b) risken för skador på betongen. För svenska förhållandet avseende skador på armering krävs det också att man har tillgång till den nya standarden SS 212540, som är den svenska tillämpningsstandarden av armeringsstandarden SS-EN 10080. a) Rekommenderade värden på minsta bockningsdiameter (= dorndiameter) ges i tabell 8.1N, men i Sverige gäller andra värden. Enligt Boverkets EKS är minsta bockningsradie minst 0,75 ggr den dorndiameter som används vid bockprovning. Värdena i BBK 04 tabell 8.6.1 är baserade på den regeln, med anpassning till ett antal standarddiametrar. Alla BBK:s värden stämmer med grundregeln enligt EKS, med ett undantag:
För ø12 anger BBK rmin = 16mm, men enligt den nya armeringsstandarden SS 212540 är dorndiametern vid provning 2ø, vilket enligt EKS skulle ge 
b) Här gäller ekvation (8.1), som ger minsta bockningsdiameter; minsta bockningsradie är således halva det värde som beräknas, lämpligen avrundat uppåt till närmaste standardradie. Här bör man även se upp med de två första strecksatserna i 8.3 (3): båda behöver inte vara uppfyllda samtidigt, det räcker med den ena eller den andra (detta är infört som rättelse i Corrigendum nr 2).
Fråga: Kan tvärkontraktionstalet antas vara 0 både vid sprucken och osprucken betong vid beräkning av plattor? Jag har letat men hittar inte något i EK2-1-1 som motsvarar punkten 6.5.2.1 i BBK 04.
Svar: I SS-EN 1992-1-1, 3.1.3(4) står det att ”tvärkontraktionstalet får antas vara 0,2 för osprucken betong och 0 försprucken betong”. I övrigt så finns det inga anvisningar som berör tvärkontraktionstalet i kapitel 5 Bärverksanalys. Anvisningen i BBK får väl anses som en konservativförenkling medan anvisningen i SS-EN 1992 är mer realistisk.
Fråga: Jag vill kontrollera 7.4.1 (4) i SS-EN 1992-1-1:2005.Deformationsbegränsningen är satt till 1/250, men jag gissar att det är längden genom 250 som menas?
Svar: Ja, det spannets längd delat med 250 som är begränsningen av nedböjningen (och överhöjning) enligt 7.4.1(4),och så står det också i klartext i paragrafen: … 1/250(en tvåhundrafemtiondel) av spannets längd.
Fråga: Enligt 6.4.4 skall armeringsinnehållet fördelas på sträckan pelardimensionen plus 3d per sida.
Hur skall armeringsinnehållet ρ beräknas i formel 6.47 för kantpelare och hörnpelare?
Beteckningar
c = pelardimension i respektive riktning
d = effektiv höjd i respektive riktning
Innerpelare c + 6d ρ = As / [(c + 6d) d]
Kantpelare
vinkelrätt kanten c + 6d ρ = As / [(c + 6d) d]
parallellt med kanten c + 3d ρ = As / [(c + 3d) d]
Hörnpelare c + 3d ρ = As / [(c + 3d) d]
Svar: För böjarmering vid hörnpelare och för böjarmering vid kantpelare vinkelrätt kanten ger avsnitt 9.4.2 anvisningar om hur den ska fördelas för att överföra böjmoment från plattan till pelaren. Det är således den armeringen med den fördelningen som kan medräknas i formeln för bärförmåga vid genomstansning. För den kontinuerliga riktningen parallellt med kanten vid kantpelare, börarmeringen över pelaren samt inom 3d vid sidan om pelaren medräknas.
Armeringsinnehållet som ska användas i formeln 6.47 beräknas sedan av det geometriska medelvärdet av armeringsinnehållen i de två riktningarna och maximeras till 0,02.
Fråga: En fråga angående miniarmering i massiva plattor. Enligt SS-EN 1992-1-1 kap 9.3 ska sekundär tvärgående armering med en area motsvarande 20% av huvudriktningen läggas in i enkelspända plattor. Gäller detta även håldäcksplattor och massiva förtillverkade enkelspända massiva plattor som gjuts ihop i fogarna vid montage på arbetsplatsen?
Svar: Det är inte rimligt att ställa krav på tvärarmering i håldäck. Det finns dock ingen särskild undantagsparagraf i kapitel 10 i SS-EN 1992 avseende det som står i avsnitt 9.3. Man bör dock kunna hänvisa till standarden för HD-plattor, EN-1168, för att kunna fortsätta tillverka håldäck utan tvärarmering.
När det gäller enkelspända massiva plattelement är läget än mer oklart. Här finns det ju egentligen inget fysiskt hinder mot att lägga till tvärarmering. Möjligen kan man även här hänvisa till någon SS-EN-standard för massivelement, om sådan finns. Alternativt gäller generellt att alla miniarmeringsregler enligt kapitel 9 bör följas om inte ”kraven på säkerhet, brukbarhet och beständighet”(se 9.1(1)P) kan påvisas på annat sätt. En särskilt utredning om detta i varje enskilt fall kan alltså vara ett sätt att slippa tvärarmeringen. Man ska dock alltid se till att inte bryta mot någon grundläggande princip i eurokoden/EKS:n.
Fråga: Kan pkt 7.3.3 (5) i 1992-1-1 anses gälla vid användning av 1992-2? I 1992-2 är 7.3.3 (5) ej nämnd i uppräkningen ”Följande avsnitt i SS-EN 1992-1-1 gäller” underkapitel 7.
I 1992-2 är dock 7.3.3 (5) inte specifikt upphävd underkapitel 7.3.3. ( Jämförelse t.ex. text under kapitel 7.4.1.)
Svar: Vi bör i första hand gå på skrivningen i förordet till 1992-2 att ”Alla relevanta avsnitt i SS-EN 1992-1-1 är tillämpliga för dimensionering av broar, såvida de inte särskilt upphävs eller ändras i SS-EN 1992-2”. Idetta fall är punkt (5) varken särskilt upphävd, jämför7.4.1, eller ersatt av en punkt (105). Det finns dessutom inget tekniskt skäl till att punkt (5) inte skulle gälla även för broar.
Det är nog en ofullständighet i listan med ”gällande avsnitt” i SS-EN 1992-2, kap. 7.
Fråga: Varför finns inte SS 137003:2008 med som ”nationell anpassning” i SS-EN 206-1? SS-EN 1992 finns den inte heller med i den nationella anpassningen. Det finns dessutom ingen notering (i bl.a. Bilaga NA) att betongkvaliteterna: C28/35; C32/40; C54/65 & C58/70 fortfarande är gällande?
Svar: I det nationella förordet i SS-EN 206-1 hänvisas till SS 13 70 03. SS-EN 1992 behöver nog knappast nämna att det kan finnas nationella anpassningar till SS-EN 206-1. Det kan för övrigt finnas nationella “anpassningar” till alla europeiska produktstandarder. Detta eftersom dessa enbart anger hur man ska prova och ange produktprestanda, och hur produktionskontrollen ska ske för att man ska få CE-märka produkten, medan prestandakrav kan ges i nationella bestämmelser o.d.
Eurokoderna är ju dimensioneringsstandarder, som hänvisar till produktstandarder. Dessa produktstandarden kan, som SS-EN 206-1, ha öppningar för nationell anpassning. Men en sådan nationell anpassning av produktstandarder anges inte som NDP i eurokoden, och har därmed inte hamnat i tillämpningsföreskriften till dimensioneringsstandarden eurokoderna (Boverkets EKS/Vägverkets ”EBS”/NA), utan den anges produktstandarden SS-EN 206-1.
Boverket har en ny EKS, som är en fullständig anpassning av BKR till eurokoderna, som är på notifiering och ska införas i början av 2011. Där ingår då även andra krav från BKR, som materialkrav och utförandekrav. Alltså även sådant som inte är direkta dimensioneringsregler (tillämpningsregler till eurokoderna). Även Trafikverket kommer att göra en motsvarande anpassning av sin VKR/”EBS”. I dessa kommer man då att hitta både dimensioneringsregler, materialkrav etc.
Vad gäller mellanliggande hållfasthetsklasser, så ser jag egentligen inget hinder att använda dessa i eurokodsammanhang. I principerna SS-EN 1992-1-1, 3.1.2 (1)P och (2)P anges vad hållfasthetsklasserna ska baseras på; karakteristisk cylinderhållfasthet och kubhållfasthet enligt SS-EN 206-1, samt att det är 28-dygnshållfastheten som avses. Hänvisning till tabellen 3.1 där hållfasthetsklasser anges är inte princip utan råd. I tabellen finns ju dessutom formler för de olika parametrarna baserat på basvärdena, karakteristisk cylinderhållfasthet och kubhållfasthet, så det är enkelt att för andra värden på dessa än de tabellerade räkna ut alla andra värden.
Fråga: På vilken nivå skall töjningen i formel (7.8) i SS-EN 1992-1-1 väljas?
Vid dimensionering av en brobana med ett T-tvärsnitt, har vi fem lager armering. Det ger därav stor inverkan vart man antar töjningarna.
Eget resonemang:
• Total armerings TP
• Medeltöjningen av effektiv betong sätts i armeringens TP
• Understa lagrets TP
• Sprickkravet antas mot närmaste verksam armering
Svar: Ekvation 7.8 ger den beräknade sprickbredden i den nivån där armeringsspänningen är beräknad, vilket ska vara i armeringens TP och med effektiva betongarean jämnt fördelad uppåt och nedåt. Har man många armeringslager innebär det att sprickbredden i nivå med lagret närmast den dragna sidan kommer att vara betydligt bredare vid böjning än i armeringens TP. Kravet på max sprickbredd som avser att skydda armeringen bör då ställas mot sprickbredden i det mest dragna lagret. Enklast bestäms den sprickbredden genom att extrapolera den beräknade sprickbredden enligt 7.8 (som avser armeringens TP) till det aktuella lagrets nivå med bas (sprickbredd = 0) i det neutrala lagret i stadium II.
Fråga: I bilaga NN i SS-EN 1992-2:2005 så talar man i tabell NN.2 om innerfack och ändfack. Är ytterfacket på en ändskärmsbro att betrakta som ett ändfack? Man har ju trots allt en slags inspänning i jorden. Tillsvidare gör vi det, men vad är korrekt?
Hur ska kritisk längd på influenslinjen bestämmas för en konsol?
Svar: Lambdametoden är framtagen för väg- och järnvägsbroar broar i längsriktningen utformade som fritt upplagda eller kontinuerliga balkar. Avviker utformningen från detta är den egentligen inte tillämplig, utan man hänvisas till att göra en verifiering med hänsyn till utmattning med den mer generella delskademetoden. För broar som inte avviker alltför mycket bör man dock kunna använda den med antagande av vissa förenklande förutsättningar, som då måste ge resultat på säker sida. Det är bara vid bestämning av korrigeringen, λ-värdet, man behöver förenkla. Som grundvärden för påkänningarna utgår man alltid från de snittkrafter som erhålls vid den mest ogynnsamma placeringen av tåglast LM71. Detta gäller för varje punkt utmed bärverket, såväl spannen som utkragningen vid ändskärmen, och den bestäms för aktuellt bärverk som det är modellerat. Ändskärmsbroar modelleras vanligen på så sätt att laster på utkragningen vid ändskärmen ingår i modellen medan det samtidigt bortses från att ändskärmen kan göra motstånd mot rotationer och vertikala translationer.
I tabellerna i NN.2 ser man att λsi för fritt upplagd, mittspann och ändspann inte skiljer sig så nämnvärt mycket. För tung trafik är skillnaden som mest 0,10 enheter för samma spännvidd. Att förutsätta det ena eller det andra ger alltså inte starkt avvikande resultat.
Ett problem med metoden som den står beskriven i eurokoden är att man använder termen ”kritisk längd på influenslinjen” vilket inte används i någon bakgrunddokumentation eller i ENV-versionen, vilket måste vara ett missförstånd hos standardskrivarna och som ger tolkningsproblem. Där används uteslutande termen spännvidd.
En ändskärmsbro är ju en fritt upplagd eller kontinuerlig bro med utkragande konsoler. I bakgrundsdokumenten till metoden (Rapport ERRI D 183/DT 346, Fatigue design of concrete railway bridges; som tillhandahålls av UIC) står inget om konsoler i brons längsriktning, däremot om konsoler i tvärriktningen. För det anges att faktorn för inspänningsmomentet kan baseras på L = 1,5 ggr utkragande längd med hjälp av värdena för fritt upplagda balkar. Då λ-värdet minskar med L är det troligen på säker sida sätta L = utkragningslängden och använda tabellen för fritt upplagda balkar för konsoler i längsriktningen.
Sammanfattningsvis kan man, om en ändskärmsbro modelleras utan att ändskärmens motstånd mot rotationer och vertikala translationer beaktas, göra enligt följande:
Enspanns ändskärmsbro – använd värden för fritt upplagda balkar
Ytterfack i kontinuerlig ändskärmsbro – använd, med undantag av stödmoment över ändstöd, värden för ytterfack i kontinuerliga balkar.
Alternativt kan man för en ändskärmsbro med ett spann för huvudspannet mellan stöden välja det λ-värde från de tre tabellerna som är högst för aktuell spännvidd. För en ändskärmsbro med mer än ett spann väljs det λ-värde av de som gäller för ytterfack och mellanspann som är högst för aktuell spännvidd.
För stödmoment över ändstöd i ändskärmsbro – L = utkragningens längd tillsammans med tabellen för fritt upplagda balkar.
Fråga: I SS-EN 1992 regleras minsta bockningsradie för armering med hänsyn till armeringens bockbarhet, betongens spjälkning etc. I BBK finns även en övre gräns för bockningsradien med hänsyn till hörnstängernas fixering, se BBK 04 avsnitt 3.9.4.2, villkor 3.9.4.2 b och c. Jag kan inte hitta något motsvarande i det nya regelverket. Får man ha hur stora bockningsradier som helst?
Svar: Någon motsvarande regel som BBK 04:s villkor 3.9.4.2 b och c finns inte. Förankring av byglar ska utföras enligt SS-EN 1992-1-1 avsnitt 8.5(2). Även där saknas dock anvisning om max bockningsradie, vilket får ses som en brist i SS-EN 1992. Konstruktören måste själv bedöma hur en stor bockningsradie påverkar förankringen.
Fråga: Det är aningen oklart för vilka fall det kan bli aktuellt med armering mot hörnavspjälkning. En figur som även visar geometrier i plan hade varit önskvärd.
Jag skulle därför vilja ha ett förtydligande när det kan bli aktuellt med armering mot hörnavspjälkning. Intressant är t.ex. vilken inverkan som lastens läge i förhållande till kanten (hörnet) har på brottet (lasten går ända ut till kanten eller ligger med visst avstånd till densamma). Då befintlig figur inte ger all information om lastens placering är det osäkert om fenomenet inträffar endast vid placering nära hörn eller även vid placering nära kant (jämför t.ex. hörn- eller kantpelare).
Resonemanget påverkar armeringens placering. Skulle gärna vilja se en figur som visar just armeringens placering i plan om nu rubricerat även gäller för last nära kant.
FÖRTYDLIGANDE AV FRÅGA:
Frågan avser SS-EN 1992-2, bilaga J.104.1 (104), (105) och figur J.107:
När är det aktuellt med en kontroll av avspjälkning av hörn?
Jag vill gärna hänvisa till Figur 6.15 i SS EN 1992-1-1. Kan läget för dessa belastade areor innebära att en kontroll av hörnavspjälkning är aktuell? Jag avser inte genomstansning utan hänvisar bara till figuren rent principiellt vad gäller lastens placering på ett bärverk.
Hur ska armering mot hörnavspjälkning utformas? Relatera gärna till en principfigur motsvarande 6.15 i SS-EN 1992-1-1. När är det INTE aktuellt med en kontroll av avspjälkning av hörn?
Svar: I första meningen SS-EN 1992-2, J.104.1(104) av den engelska versionen står det ”edge” där det på svenska står hörn. Samma skillnad finns i titeln till figur J.107. Den engelska texten har alltså en lydelse som inte begränsar fenomenet till hörn. Därmed är jämförelsen med hörnspjälkning inte längre aktuell.
Hur armeringen ska utformas framgår av (104).
Det är alltid aktuellt med en kontroll av detta men ibland (kanske ofta) kommer minimiarmeringskrav att ge en större armeringsmängd.
Fråga: Hur bestämmer man vilken utförandeklass som skall väljas till betong i Eurocode?
Svar: Eurokod 2, SS-EN 1992-1-1, behandlar inte utförande men det hänvisas till utförandestandarden SS-EN 13670. I den standarden ges de olika utförandeklasserna och vad som gäller för dessa. Obeservera dock att dessa utförandeklasser inte är de samma som utförandeklasser enligt BBK som baserades på kompetens hos utförare och leverantör. Kompetensklasser beskrivs nu istället i den svenska tillämpningsstandarden SS 137006 och i AMA.
En artikel om utförandestandarderna där de nya och gamla utförandeklasserna, och kompetensklasserna tas upp finns på www.eurokoder.se; Eurokodnytt nr 4 2011. Kompetensklasserna och hur de används finns bl.a. i bilaga EB/1 i AMA Anläggning 10. I nya AMA Hus är det bilaga ES/1. Utförandeklass enligt SS-EN 13670, som styr kontrollen, ska enligt Trafikverkets och Boverkets regler vara lägst klass 2 i Sverige.
Den svenska tillämpningsstandarden SS 137006 samt AMA är inte införlivade i Boverkets regler och får därför inte betraktas som en del av eurokodssystemet. Man kan därför endast utnyttja dessa dokument om man är helt säker på att vad man väljer eller gör inte strider mot eurokodsystemet.
Fråga: Har en fråga som rör vertikalkopplingar i prefabricerade hus högre än 4 våningar.
I SS-EN 1992-1-1 avsnitt 9.10.1 Allmänt, står följande:
”Bärverk som inte dimensioneras för olyckslaster ska ha ett lämpligt system av sammanhållningsarmering för att förhindra fortskridande ras genom att möjliggöra alternativ lastnedföring efter lokal skada.”
I avsnitt 9.10.2.5 Vertikala dragband, står följande:
”I elementbyggnader bör pelare och bärande väggar förses med vertikala dragband, om byggnaden har minst 5 våningar, för att begränsa skadorna på ett bjälklag vid förlust av en pelare eller vägg i våningen under. Dessa dragband bör utgöra del av ett alternativt lastnedföringssystem som kan överbrygga det skadade området.”
Om man antar att man har ett kontorshus som skall byggas i prefab med fasadpelare ut mot en gata. Pelarna och infästningarna är dimensionerade för påkörningslaster enl. SS-EN 1991-1-7. Skall man ändå anse att man skall kunna slå bort en av dessa pelare? Vad är då vitsen med att dimensionera pelarna för påkörning om man ändå skall räkna med att man kan slå bort en pelare? Med stöd av det som står under avsnitt 9.10.1 Allmänt behövs inte vertikala kopplingar till ovanliggande pelare, eftersom pelarna är dimensionerade för olyckslasten som i detta fall är påkörningslaster. Är detta en rätt tolkning?
Svar: Reglerna i SS-EN 1992-1-1 liknar dem som vi haft tidigare, d.v.s. att man antingen dimensionerar bärverksdelar för att motstå olyckslast, eller förser konstruktionen med schablonmässig sammanhållningsarmering för att förhindra fortskridande ras. Som du själv påpekar framgår detta tydligt av 9.19 (1)P. Det som står i (2) – (5) är exempel på sådan armering som behövs när man inte dimensionerar för en specifik olyckslast.
Överordnat gäller val av sätt att säkra mot olyckslast eller skador enligt avsnitt 3.3 och 3.4. i SS-EN 1991-1-7, där endera av tre alternativ kan väljas; dimensionera väsentliga byggnadsverksdelar för olyckslast, dimensionera för för lokal skada (t.ex. bortslagen pelare) eller använda schablonregler för att ge byggnadsverket robusthet (t.ex. förband).
Väljer man att inte dimensionera väsentliga byggnadsdelar för olyckslast eller se dem som bortslagna ska reglerna i SS-EN 1992-1-1, 9.10 kombineras med reglerna i SS-EN 1991-1-7, bilaga A där kraven beror på vilken konsekvensklass som byggnaden tillhör.
Observera att om man väljer att dimensionera för olyckslast ska alla väsentliga byggnadsdelar dimensioneras för detta, inte bara den mest utsatta som i detta fall fasadpelaren mot gatan. Lasterna ges av anmärkning 1 till SS-EN 1991-1-7. 3.3. Samma princip gäller även vid lokal skada. Det är inte bara fasadpelaren mot gatan som ska antas vara bortslagen.
Ett alternativ kan vara att man för fasadpelarna tillämpar påkörningslast eller bortslagning och för byggnaden i övrigt tillämpar schablonreglerna.
Fråga: Fråga angående väggskivors upplag, vid dimensionering med fackversmodell:
Är det en icke motstridande uppgift att använda principerna för upplagstryck vid skivor som ansluter mot bjälklag enligt ex. diagram 6.6:23 och 6.6:25 i betonghandboken Kap 6.6. Skivor?
Kapaciteten för upplagstryck för skivor är betydlig högre om man använder uttrycken i BBK och betonghandboken Kap 6.6.5.2 än de om noder i SS-EN 1992-1-1 6.5.4.
I betonghandboken får man mer nyanserat även tillgodoräkna sig anslutande bjälklag i tryckkoefficienten k, med hänvisning till Nylander. H publikation 66 & 113 BYV KTH.
Hittar inget om detta i Svenska Betongföreningens handbok till SS-EN 1992-1-1, endast en kort kommentar angående möjlighet till tryckarmering för upplag och trycksträvan.
Bifogar beräkning med jämförelse BBK/Betongandboken mot SS-EN 1992 Kap 6.5.4.
Beräkningen visar att Figur 6.6.25 kurva A1 (anslutande bjälklag och särskild tryckarmering) ger värden nära de som motsvarar triaxiellt spänningstillstånd enligt 6.5.4 (6).
D.v.s. att man med anslutande bjälklag och armeringsbyglar för omslutning i nod-zonen (I princip enligt Figur 6.6:26 i BH) uppfyller ett triaxiellt spänningstillstånd och kan använda principen i Betonghandboken?
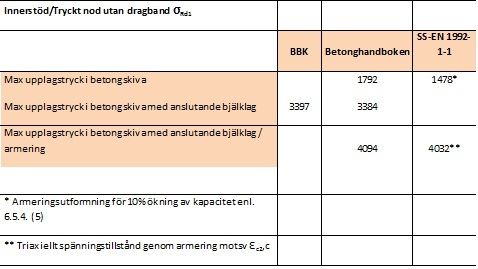
Svar: Betonghandbokens metod bygger på teori med tryckbåge medan SS-EN 1992-1-1 redovisar regler för användning av fackverksmetoden. Observera att SS-EN 1992-1-1 inte anger att fackverksmetoden måste användas för dimensionering av höga balkar. I avsnitt 5.6.4 anges att fackverksmetoden får användas för brottgränsdimensionering av diskontinuitetsområden (vilket ju en hög balk är).
Jag tolkar det som att tryckbågsmetoden enligt Betonghandboken inte är en motstridande metod. Förutsättningen är att man använder sig av hållfasthetsvärden och lastvärden enligt Eurokoderna.
Ska man använda tryckbågsmetoden (med värden enligt eurokoden) så måste det bli den för hela skivan, inte bara själva upplagstrycket.
Däremot är det fullt tillåtet att i en fackverksmodell utnyttja möjligheten att tillgodoräkna sig triaxiellt spänningstillstånd eller andra gynnsamma förhållanden enligt Kap 6.5.4(5) och (6).
Fråga: Vad är minsta armeringsmängd i plattbärlags tvärrikting enligt eurokod?
Svar: När ett plattbärlag kompletteras med en pågjutning till att bli det färdiga bjälklaget utgör det en del av en massiv platta. Minimiarmering för massiva plattor regleras i SS-EN 1992-1-1 enligt avsnitt 9.3. Därunder i paragraf 9.3.1.1(2) anges att en area om minst 20 % av huvudarmeringens bör läggas som sekundär tvärgående armering. Anledningen till detta är att säkerställa en plattverkan och fördelning av laster över en större plattbredd. Tvärameringen placeras med fördel i pågjutningen över ett plattbärlag.
Vidare anger paragraf 9.3.1.1(3) även vad största centrumavståndet för den sekundära armeringen i tvärled bör vara. För jämnt utbredd last är det 3,5h, dock maximalt 450 mm, där h är plattjockleken. Inom områden med koncentrade laster och inom områden med maximimoment minskas största centrumavstånd till 3h, dock maximalt 400 mm.
Fråga: Frågan gäller SS-EN 1992-1-1, 9.7 (1), och avser hur man beräknar ytarmeringen enligt denna punkt och var denna placeras? Ett klarläggande önskas då vår tolkning gett väldigt stora minimiarmeringsmängder för grova konstruktioner.
Svar: Armeringsmängden ska i vardera ytan vara 0,001Ac (ursprungligen stod här 0,1 %, men det är rättat), dock minst 150 mm2/m. Armeringen placeras som ett rutnät i vardera ytan. Armeringsmängden är nationellt valbar, men Sverige har valt att använda rekommenderat värde (gäller både byggnader och broar).
Kommentarer till denna minimiarmering finns i t.ex. Svenska Betongföreningens handbok till SS-EN 1992, sidan 1-120.
Fråga: Nedan är tabell 6.3N hämtad ur EN 1992-1-1, Kap 6.8.4.
Här anges ”diameter of the mandrel” vilket direktöversatt blir “diameter av dornet” alltså bockningsdornets diameter. Vid bockning är dornens diameter mindre än armeringsjärnets slutgiltiga bockningsdiameter som man vill erhålla. Detta får till följd att den svenska översättningen ger ett hårdare krav än den engelska. Det verkar inte OK i min mening.
Hur ska detta tolkas? Finns det något korrigendum som redan belyser detta? Vart vänder jag mig för dessa frågor?
Svar: Bockningdiameter och dorndiameter för att åstakomma bocken har samma värde, se SS-EN 1992-1-1, avsnitt 8.3.
Jag antar att frågeställaren avser skillnaden mellan minsta bockningsradie och dornradie enligt BBK 04, Kap 8.6.1. Observera att dornradien avser bockningsprov. Vid bockning av armering som ska användas i konstruktioner måste dornradien (och därmed den slutliga bockningsradien) vara 1,5 gånger större än den som används vid bockningsprov.
Fråga: Vi har många och långa diskussioner på företaget hur begreppet ”minimiarmering” ska behandlas i Kap 9. Vi landar sällan i något som vi alla kan förstå och tolka. Enligt BKR har vi förut gjort tolkningen att ett brottsgränstillstånd för någon given konstruktion avgör behovet av armering.
Som komplement till kraftfördelningen p.g.a brottslast enligt ovan har man studerat eventuellt behov av säkerhets-/sammanhållande armering för ras (seghet ex.vis x/d<0,45), och i ett senare bruksgränstillstånd, ett armeringsbehov för att förhindra för stora sprickor, eller för stora deformationer. Då har man också med ganska enkla insikter kunnat göra följande iakttagelser:
- Är det stor egentyngd i förhållande till belastningen blir det en del armering i bruksgränstillstånd för just denna last.
- Har man högre balk (t ex) och därmed större inre hävarm får man mindre armering allt som oftast.
- Om inget framräkningsbart tillstånd p g a yttre last kan studeras, och man ändå har ”tvång” kan man tillämpa ”minimiarmering för sprickviddsbegränsning”.
Nu till Eurokoden;
I kapitel 9 finns för detaljutformning för t ex balkar (kap 9.2) – resonemanget gäller generellt – att för att konstruktionen/balken ska få räknas armerad, ska den innehålla en viss mängd armering. Detta oavsett om ett framräknat gränstillstånd borgar för ett mindre behov av armering. Rätt tolkat? I formel (1) kan ses att den inre hävarmen ”d” ingår som parameter i beräkningen av mängden miniarmering och det strider mot pkt 2 i BKR-resonemanget ovan, att ju högre balk man har, desto mindre armeringsbehov. I Eurokoden spelar detta ingen roll, högre balk ger mer armering. Rätt tolkat? Man kan få oerhörda mängder armering, när det ”gamla” brottresonemanget kanske bara gett ett eller två armeringsjärn som behov, just för att större tvärsnitt ger mer armering.
Skulle man ändå vilja behålla en liten mängd armering, t ex vid dimensionering av en vertikalbelastad vägg, så ska man då tillämpa kapitel 12 – lätt armerad och oarmerad betong, med helt andra partialkoefficienter. Vår vana trogen är vi ganska trygga med lite armering i vertikalled i en tryckt vägg men nu ställs detta på sin ända. Samma resonemang där, ju tjockare vägg, desto mer miniarmering för att den ska får räknas som ”armerad”.
Resonemanget med ”bärande” minimiarmering känns igen från gamla Bronormen. Kan detta vara en rätt iakttagelse? Att det nu kommit in i husbyggnationen.
Som konstruktörer blir vi ganska hårt åtgångna av erfaren produktionspersonal när vi både ökar armering i horisontalled, och nu även i vertikalled, vad gäller väggar som exempel.
Hur ska vi resonera kring BÄRANDE minimiarmering respektive SPRICKVIDDSBEGRÄNSANDE armering? Kan man fortfarande resonera att brottsbelastningen ger brottarmering, och bruksgränstillstånd ger nödvändig armering med hänsyn till sprickor och deformationer, och om inget annat kan beräknas, armeras enligt sprickviddsbegränsande armering?
Under formlerna i Kap 9.2 kan läsas:
”Alternativt får, för bärverksdelar av mindre betydelse för vilka viss risk för sprödbrott kan accepteras, Asmin sättas till 1,2 gånger den area som erfordras vid verifieringen i brottgränstillstånd.
(2) Tvärsnitt som innehåller mindre armering än Asmin bör betraktas som oarmerade”
Detta kan lätt tolkas att trots alla partialkoefficienter och materialparametrar i brottsgränstillstånd, BÖR man öka brottarmeringen 20%. Rätt tolkat?
Svar: All minimiarmering bygger på principen att armerad betong ska kunna få ett segt brott. Om armeringen inte kan bära den last som gör att betongen spricker, kan det ske en plötslig kollaps och ett allt annat än segt brott. Se 9.1 (3).
Detta är lätt att förstå för en böjd balk och uttrycket för minimiarmering i balkar (9.2.1.1) bygger direkt på denna princip. Uttrycket kan härledas för ett rektangulärt tvärsnitt där sprickmomentet antas svara mot dragspänning fctm i betongen och armeringen ska klara detta moment i sprucket tvärsnitt med spänning fyk. För andra tvärsnitt än rektangulära blir uttrycket lite approximativt. Konsekvensen blir naturligtvis att armeringsbehovet ökar med ökande balkhöjd, eftersom sprickmomentet då ökar.
Alternativet med 1,2 ggr brottgränsarmeringen är ett mer trubbigt verktyg, och kan inte alltid garantera ett segt brott. Det bör bara användas för sekundära balkar.
I övrigt ska minimiarmeringen enligt 9.1 (3) även förhindra grova sprickor och kunna ta upp tvångskrafter. Här blir det lite mer diffust, och det är ju inte alltid säkert att minimiarmeringen räcker. Den är dock alltid ”bättre än inget”.
Fråga: I SS-EN 1992-1-1:2005/AC:2010 Figur 6.18 är avståndet mellan pelarens och kapitälets ytterkanter IH > 2,0 hH men i bildtexten är IH > (d + hH). Är det IH >2,0 hH som gäller även i bildtexten?
I (10) anges att "Reglerna i 6.4.2 och 6.4.3 är även tillämpliga vid kontrollsnitt inom kapitälet ..." Hur hanteras fallet när IH är något längre än 2hH och rcont.int faller utanför kapitälet? Är det underförstått att rcont.int alltid hamnar inom kapitälet?
A – grundkontrollsnitt for runda pelare, B – belastad area, Aload
Figur 6.18 – Platta med förstorat kapitäl där IH > 2(d+hH)
Svar: Det ska stå 2hH även i figurtexten.
Om IH > 2hH gäller att stanskontrollen görs för d+hH .Att rcont.int faller utanför kapitälet spelar ingen roll. Det som avgör är att en trycksträva kan gå rakt från armeringen ner till pelar”roten” och det kan den alltid så länge IH > 2hH. Skulle IH vara 2hH går det inte, men det är heller inte ”tillåtet”.
Fråga: Jag undrar över vertikalkopplingar i pelare, se SS-EN 1992-1-1 avsnitt 9.10? Om vi antar att vi har balkonger som bärs av betongpelare i framkant och av fasaden i bakkant, byggnaden är >= 5 våningar. Behöver man koppla pelarna vertikalt eller kan man anta att balkongerna kan rasa ner eftersom de inte tillhör "huvudsystemet"? Alternativ lastnedföringssystem är inte möjligt i detta fall.
Svar: Balkonger är inte undantagna utan man bör se till att även dessa klarar en olycka där en pelare slås bort. Ett kontinuerligt dragband eller koppling som gör att balkongen ovan en bortslagen pelare kan hänga kvar bör därför finnas enligt 9.10.2.5(1) eller om jämvikt kan erhållas med ”tre ben” enligt 9.10.2.5(2).
En alternativ lastnedförning enligt 9.10.2.5(3) behövs bara om pelarna står på andra fribärande konstruktionselement som t.ex. balk eller bjälklag.
Observera att SS-EN 1992-1-1 Kap 9.10 enbart gäller i det fall byggnaden inte dimensioneras för en specifik olyckslast, t.ex. genom att pelarna kan bli påkörda. Även om det inte finns risk för påkörning finns det ytterligare robusthetskrav i SS-EN 1991-1-7 för att minimera risken för fortskridande ras. Dessa varierar med bl.a. byggnadens höjd. Enligt bilaga A (informativ) hör en bostadsbyggnad med 5 våningar till konsekvensklass 2a, och utöver kraven i SS-EN 1991-1-1, Kap 9.10 bör då även SS-EN 1991-1-7, A.5.1 och A.5.2 tillämpas.
Fråga: Ekvation 8.5 är en begränsning av produkten α2, α3, α5 och som gäller för beräkning av förankringslängd enligt Kap 8.4.4
Vid beräkning av skarvlängd enligt Kap 8.7.3 (1) hänvisas till Tabell 8.2. Men gäller begränsningen enligt EKV 8.5 även i skarvlängdsfallet?
Svar: Huruvida EKV (8.5) ska gälla även vid skarvning är oklart.
I 8.7.3 (1) står att α1, α2, α3 och α5 bestäms enligt Tabell 8.2. Faktorerna beskrivs i 8.4.4 (1), tillsammans med begränsningen enligt ekvation (8.5). Man kan då tolka det som att beskrivningen inklusive ekvation (8.5) gäller även vid skarvning. En annan tolkning är att hänvisningen i Kap 8.7.3 endast gäller tabell 8.2, inte det övriga som står i 8.4.4 (1), d.v.s. inte EKV (8.5).
Frågan bör avgöras av berörd myndighet.
Eftersom det bara hänvisas till Tabell 8.2 och inte till avsnitt 8.4.4(1) borde inte uttrycket (8.5) gälla för tillämpningen enligt 8.7.3(1) . Hade motsvarande stått i t.ex. en tabellnot hade slutsatsen blivit en annan. En annan sak som talar mot tillämpning av uttryck (8.5) är att α3 är något modifierad.
Det är dock inte möjligt att utan en noggrannare utredning avgöra vad som gäller. För att kunna göra det behöver frågan tas upp med CEN, Europrean Committee for Standardization.
Fråga: Jag har en fråga om tolkning av en artikel i SIS-CEN/TS 1992-4-1 som jag hoppas Ni kan/får svara på.
I artikel 5.2.2.2 står det ordagrant i vår utgåva "The load distribution to the fasteners may be calculated analogous to the elastic analysis of reinforced concrete using the following assumptions (see Figure 8) : a) the axial stiffness EsAs of all fasteners is equal. In general As may be based on the nominal diameter of the fastener and Es = 210 000 N/mm2
Nu lämnar ju detta stycke en hel del utrymme för tolkningar och vi har olika åsikter här på kontoret.
– Å ena sidan så finns det åsikter som säger att stycket bara föreslår en väg att räkna med elastiska ankare, men att styvheten i dom får man som ingenjör göra en bedömning av (här finns ju dragprov på olika ankartyper från diverse leverantörer att använda sig av som ger en väsentligt lägre styvhet än den föreslagna. Detta blir ju då en kombination av
– Sedan finns det ju andra tolkningar som säger att man får räkna med elastiska ankare men då skall man använda 210 MPa styvhet.
– Den tredje åsikten (som kanske är mest försiktig) är att man bör vid elastiska ankare räkna med jämnstyva ankare i hela strukturen (eller i alla fall de ankare som delar funktion) så att ingen del blir väsentligt mycket vekare än någon annan del med samma funktion. Samt att man använder 210 MPa istället för någon uppmätt från experiment hos leverantören.
Svar: Texten är helt klar och lämnar inte något utrymme för tolkning.
Det handlar om beräkning av krafter i ett förband där vissa skruvar tar drag. En del av tvärsnittet kan vara tryckt, såsom i figur 8 och 9, men det kan också vara så att alla skruvar tar drag. Hur som helst, vad som sägs är att fördelningen av krafter kan beräknas enligt en elastisk modell med linjär töjningsfördelning, analog med den man använder för armerade betongtvärsnitt i bruksgränstillstånd. En skillnad mot betongtvärsnittet är dock att man här inte räknar med skruvar i tryckt betong, medan man i betongtvärsnittet även kan medräkna armeringsstänger i tryckzonen.
En förutsättning för modellens linjära töjningsfördelning är att fotplåten är tillräckligt styv för att inte böjas plastiskt (5.2.2.4). Om detta inte är uppfyllt kan man kanske tänka sig en plastisk modell, men detta framgår inte.
Vänligen notera att SIS-CEN/TS 1992-4-1 är ingen eurokod. Den är en teknisk specifikation som eventuellt kan komma att införlivas i eurokoden för betong. Den kan dock användas som en vägledning för att behandla den här typen av frågor.
Fråga: Bifogar beräkningar av sprickbredder för ett betongbjälklag. Jämförelse SS-EN 1992-1-1 och BBK 04.
SS-EN 1992-1-1 ger orimligt små sprickbredder. Tacksam för synpunkter.
Sprickbreddsberäkning Jämförelse EUROKOD 2 OCH BBK 04
2BBK04
2BBK04_2
2EK2
2EK2_2
BKK04
BBK04_2
BBK04_3
PsEK2
PsEK2_2
SsEK2
SsEK2_2
Svar: Efter en kontrollberäkning har vi kommit fram till liknande resultat.
SS-EN 1992-1-1 ger i många fall mindre beräknad sprickbredd än BBK 04, men det finns också fall där motsatsen gäller. Det förra är t.ex. vanligare vid liten tvärsnittshöjd, det senare vid stor tvärsnittshöjd.
Om man vill hävda att SS-EN 1992-1-1 ger ”felaktiga” resultat bör man jämföra med försöksresultat, inte med beräkningar enligt BBK 04. Försöksresultat visar alltid mycket stor spridning, och det finns ingen modell för sprickbreddsberäkning som kan beakta alla parametrar med god överensstämmelse.
Jämförelser med sprickbredder i verkliga konstruktioner har visat att beräknade värden kan vara flera gånger större än de som kan uppmätas i konstruktionen. Till detta kan finnas flera förklaringar som det inte finns utrymme att gå in på här. Jämförelserna har hur som helst inte tytt på att de beräknade värdena skulle vara för små. Dessutom ska man ha klart för sig att kraven alltid avser beräknad sprickbredd, inte verklig.
Fråga: Jag vill ha mer belysning om täckande betongskikt.
Enligt definition I SS-EN 1992-1-1 Kap (4.4.1.1)
Täckande betongskikt är avståndet mellan ytan på den armering som betraktas och närmaste betongyta (inklusive förekommande byglar eller ytarmering).
Enligt exempel som finns i svenska betongföreningens handbok till SS-EN 1992-1-1 (volym II) sidan A-5 står tydligt att byglar ingår i täckande betongskikt.
Jag vill veta vad gäller vid betongbalk med byglar.
Svar: Definitionen av täckskikt i SS-EN 1992-1-1, Kap 4.4.1 gäller och i handboken står ingenstans att ”byglar ingår i täckskiktet”. Kraven på minsta täckskikt ska vara uppfyllda för både byglar och huvudarmering. Man måste hålla isär de två kriterierna för minsta täckskikt:
1. beständighet (exponeringsklass), Cmin,dur = enligt tabell i EKS 8
2. vidhäftning och förankring, Cmin,b = stångdiametern
I handbokens exempel är det krav 2 som blir avgörande, eftersom balken befinner sig i en exponeringsklass där Cmin,dur = endast 10 mm. Med huvudarmering Φ20 och byglar Φ10 kan man då säga att byglarna ”ryms” inom täckskiktet för huvudarmeringen, men detta gäller naturligtvis inte generellt, utan endast om huvudarmeringens dimension är minst dubbelt så stor som byglarnas. Om byglarna vore t.ex.Φ12 måste huvudarmeringens täckskikt vara minst 24 mm för att byglarna ska få tillräckligt täckskikt 12 mm.
I det nominella täckskiktet, det täckskikt som anges på konstruktionshandlingar, ingår även en tolerans, ΔCdev, enligt 4.4.1.3.
Fråga: Enligt Bilaga C (Normativ) i SS-EN 1992-1-1 får man använda armering som har en karakteristisk flytgräns 400-600 MPa. I EKS 8 har man satt att flytgränsen till max 500 MPa. Ska jag tolka att man i Sverige bara får använda armering som har en karakteristisk flytgräns inom 400-500 MPa?
Svar: På första sidan i avdelning D i EKS 8, Kap. 2.1.1 – Tillämpning av SS-EN 1992-1-1 – Allmänna regler, står att fyk begränsas till 500 MPa. Samtidigt står att rekommendationen i 3.2.2 2(P) används, vilket innebär att dimensioneringsreglerna är giltiga för 400 ≤ fyk ≤ 600 MPa.
Denna begränsning infördes ensidigt av Boverket i EKS 8. I EKS 9 plockades den bort igen. Observera att denna begränsning inte finns i Vägverkets/Trafikverkets motsvarande föreskrift.
Ett väsentligt skäl till att inte ha samma relativa kam-area för stål med olika sträckgräns är att kraften dessa ska överföra skiljer sig åt. Ett alternativ kan naturligtvis vara att kräva samma kam-area för alla stålkvaliteter utgående från stålet med högst sträckgräns. Den kamarea som anges i SS-EN 1992-1-1 är avsedd för fyk = 500 MPa.
I reviderad EKS, EKS 9, anges i avdelning D, kap. 2.1.1, 3.2.2(3)P
9b § Armering med sträckgräns, fyk= 600MPa får användas om relativ kam-area, fr ≥ 0,11.
Fråga: Två frågor om förankring av armering en SS-EN 1992-1-1:
I Figur 8.3 visas måttet a. Menas fria avståndet till närmaste järn, eller som i BBK 04 "avståndet mellan stänger för vilka vidhäftning utnyttjas på samma sträcka”, Figur 3.9.1.2a-b i BBK 04.
Tvärgående armering som inte är svetsad: i BBK 94 fanns meningen "som inte är utnyttjad för annan kraftupptagning". Den meningen var borttagen i BBK 04. Hur är det i SS-EN 1992? Får t.ex. i en balk byglar som behövs för att ta upp tvärkraften medräknas som tvärgående armering? Hur är det om byglarna inte behövs för tvärkraften, utan är minimiarmering enl. avsnitt 9.2.2 ?
Svar: Svaret på den första frågan bör vara närmaste järn för vilket vidhäftning utnyttjas, även om detta inte framgår klart i SS-EN 1992.
Andra frågan: armering som är utnyttjad för annan kraftupptagning, t.ex. för att ta tvärkraft, bör inte samtidigt tillgodoräknas som tvärarmering. En minimiarmering, som inte behövs med hänsyn till bärförmågan för tvärkraft eller något annat, bör däremot kunna tillgodoräknas. Det innebär t.ex. att VRd,c ska vara tillräcklig för att klara aktuell tvärkraft.
Fråga: Hur skall man tolka Eurokod när man kontollerar befintliga betongkonstruktioner för en ny last? Det som ofta blir problem att uppfylla är just miniarmeringen vertikalt i balkar och väggskivor.
Skall man uppfylla miniarmeringen kan man i stort sett inte bygga om något, utan att förstärka med kolfiber eller riva.
I ”Svenska Betongföreningens Betongrapport nr 15 Volym 1” s 1-117 (fotnot), står det något om att minimiarmeringen bara skall gälla där tvärkraftsarmering behövs? Kan man använda sig av detta?
Svar: För det första står det inte i handboken att minimiarmeringen ”bara skall” gälla där tvärkraftsarmering behövs. Det som står är att detta var ett förslag från arbetsgruppen, som dock inte anammades av Boverket.
För det andra så gäller Eurokoderna i princip för nya konstruktioner, men inte uttryckligen för kontrollberäkning av befintliga konstruktioner. När det gäller broar har Trafikverket regler om klassningsberäkningar, men för husbyggnader är det oklart vad som gäller. För närvarande finns bara Eurokoderna att gå efter, och befintliga konstruktioner uppfyller då sällan alla krav på minimiarmering.
Det kan nämnas att ett arbete med en ny Eurokod för Kontrollberäkning av befintliga konstruktioner (Assessment of existing structures) har påbörjats, samt att en reviderad SS-EN 1992 kommer att få ett avsnitt på samma tema. Dessa nya och reviderade Eurokoder kommer dock förmodligen inte ut förrän om flera år.
Vi kan inte ge något definitivt svar på hur man ska göra vid ombyggnader där man är tvungen att kontrollberäkna eller dimensionera för ändrade förutsättningar i något avseende, t.ex. ökad last, håltagning e.d. Där förändringen inte medför ökade snittkrafter eller spänningar bör den gamla konstruktionen duga, men vid ökade snittkrafter/spänningar kan Eurokodens krav på minimiarmering medföra behov av förstärkning, även om bärförmågan skulle vara tillräcklig med befintlig armering.
Det viktigaste är dock att uppfylla krav på bärförmåga. Där armeringen inte når upp till minimikraven måste konstruktören bedöma huruvida armeringen i så fall behöver förstärkas, med hänsyn till vilka konsekvenser eventuella grova sprickor m.m. kan ha på beständighet och andra funktionskrav. En annan viktig sak att beakta är möjligheten till segt brott, vilket är en viktig grund för Eurokodens krav på minimiarmering.
Verifiering av bärförmåga regleras i bland annat plan- och bygglagen. Där (1 kap. 4 §) framgår att krav på bärförmåga även gäller vid ändrad användning av ett byggnadsverk eller ändrad funktion. Om lasterna ökar måste det verifieras att bärförmågan fortfarande är större än lasteffekten (se avdelning A, § 1 i EKS ). Verifiering av bärförmåga sker mot det regelverk som gällde när byggnadsverket eller byggnadsverksdelen en gång uppfördes. Om lasteffekten visar sig vara större än bärförmågan behöver en eller flera delar av byggnadsverket förstärkas, bytas ut eller så måste det kompletteras med nya bärande delar. Bärförmågan hos dessa förstärkta eller nya delar måste verifieras enligt vid ändringen gällande regelverk. Det är dock inte tillåtet att blanda olika regelverk när bärförmågan verifieras. Till exempel kan inte lasteffekter beräknas enligt BKR och bärförmågan enligt EKS och eurokoderna när krav på bärförmåga verifieras.
Enligt plan- och bygglagens 8 kap. 7 § och plan- och byggförordningens 3 kap. 23 § ska hänsyn tas till ändringens omfattning och byggnadsverkets förutsättningar när kraven i byggregelverket tillämpas. Om det kan antas att byggnadsverkets bärförmåga ändå blir godtagbar kan avsteg från krav enligt t.ex. EKS och eurokoderna göras om byggnadsnämnden så beslutar.
Fråga: Jag önskar hjälp med tillämpning av SS-EN 1992-1-1:2005 Figur 6.6 - Tvärkraftsarmering vid korta skjuvspann med direkt strävfunktion.
Extra "spjälkarmering" ska beräknas enl. Formel 6.19.
Formel 6.19 ger att = As f (1/sin α).
Formel 6.19 ger att armeringsbehovet ökar med lutningen på skjuvarmeringen vilket är felaktigt.
Lutande byglar är effektivare än vertikala eftersom trycksträvan är lutande.
I Betongföreningens handbok 6.2.3 Tvärkraftsarmering vid last nära upplag och figur 6-9 konstateras också att formel 6-19 inte är korrekt men något förslag på lösning ges inte.
Armeringen kan möjligen vara relevant för en fast punktlast för t.ex. en huspelare på en balk. För rörliga laster som för trafik på en bro förefaller undersökningen överflödig då mängden skjuvarmering inte bör kunna öka när punktlasten kommer så nära stöd att punktlasten kan bäras direkt till stöd med en trycksträva. Vänligen klargör hur problemet ska behandlas.
Svar: Om man ser armeringen som en ren spjälkarmering borde en lutande armering vara minst lika effektiv som en vertikal, och nödvändig area borde därför inte bli större vid lutning. I SS-EN 1992-1-1 ses den dock bara som en ren skjuvarmering, som ska kunna ta en andel, beta, av tvärkraften. Av vertikal jämvikt följer då att lutning ger större area.
Beträffande rörliga punktlaster ökar armeringsbehovet per längdenhet när lasten närmar sig upplaget, men endast marginellt såvida inte balken har mycket kort spännvidd i förhållande till höjden. Att regeln skulle vålla stora problem för rörliga punktlaster kan jag därför inte hålla med om.
Jag håller med frågeställaren om att en lutande armering borde vara minst lika effektiv vid given area, men f.n. finns ingen formell möjlighet att tillgodoräkna sig detta. Det som står i handboken är endast att det för last mycket nära upplaget vore bättre med en horisontell armering, t.ex. enligt regler för sekundärarmering i konsoler, J.3.
Fråga: Försöker komma fram till vad det är som gäller för minimiarmering vid förhindrad krympning och hittar ingen hänvisning till relevant litteratur. Har använt formel i Svenska Betongföreningens Handbok men den ger orimligt mycket armering. Har ni några andra sätt att beräkna minimiarmeringen vid krympning?
(OBS! Den formel som frågeställaren hänvisar till är samma formel som återfinns i SS-EN 1992-1-1.)
Svar: EKV (7.1) i SS-EN 1992-1-1 ger minimiarmering för begränsning av sprickbredder. Den bör då även användas vid t.ex. förhindrad krympning. Formeln liknar motsvarande formel i BBK 04 med skillnaden att dragkraften omedelbart före uppsprickning enligt SS-EN 1992-1-1 räknas med hela den dragna betongarean medan den enligt BBK 04 beräknades med en effektiv betongarea.
Detta har lett till att det oftast behövs betydligt mer minimiarmering enligt SS-EN 1992-1-1 än vad som behövs enligt BBK 04, särskilt vid tjocka tvärsnitt. Från svensk sida har man föreslagit en ändring av formeln så att den mer liknar vår tidigare formel med effektiv betongarea. Tills vidare är det dock EKV. (7.1) i SS-EN 1992-1-1 som gäller eller alternativt en ”noggrannare beräkning”, som det står i SS-EN 1992-1-1 avsnitt 7.3.2(2). Ingen hänvisning till andra beräkningsmetoder ges, men när det gäller inverkan av förhindrad krympning kan en icke-linjär numerisk analys med FEM vara ett sätt. Tyvärr finns det ingen enkel handberäkningsformel tillgänglig.
Fråga: Jag arbetar med att specificera armering och jag behöver veta vilka bockningsradier jag ska använda mig av om det hänvisas till SS-EN 13670.
Konstruktören brukar skriva ut bockningsradierna i föreskrifterna men det finns konstruktörer som inte vill (eller kan) svara på det, och i stället tycker att jag borde veta det.
Jag brukar använda mig av BBK 04 när det inte anges i föreskrifterna, vilket jag antar fungerar alldeles utmärkt. Kan jag även i fortsättningen använda mig av den?
Svar: För nya betongkonstruktioner i Sverige gäller SS-EN 1992-1-1 med tillhörande nationella val, vilket för alla typer av konstruktioner förutom vägbroar ges i Boverkets gällande EKS. För vägbroar gäller Trafikverkets föreskrift. BBK 04 gäller inte längre.
I SS-EN 1992-1-1, avsnitt 8.3 ges regler för tillåtna dorndiametrar (dorndiameter = 2 x bockningsradie). I EKS 8 ges nationellt valda parametrar som gäller för detta avsnitt. För svenska förhållanden finns det även en armeringsstandard SS 212540, som är tillämpningsstandard till europeiska armeringsstandarden SS-EN 10080, och som också innehåller råd om bockningsradier m.m.
OBS! SS 212540 är varken granskad eller accepterad av Boverket och ingår inte i systemet med EKS (Boverkets föreskrifter och allmänna råd om tillämpningen av eurokoderna) och själva eurokoderna med tillhörande hjälpstandarder. I SS 212540 finns rekommenderade dorndiametrar för bockningsprov. Om man utgår från dessa dorndiametrar när man specificerar bockningsradier är det viktigt att säkert veta att bockningsprov för den valda stålkvaliteten gjorts med dessa diametrar och inte med de större diametrar som anges i t.ex. SS-EN 1992-1-1 eller i SS-EN 10080.
Fråga: Jag undrar var man hittar γsd och vad den beaktar i utrycken nedan i SS-EN 1992-2:2005?:

Följdfråga efter svar: Det betyder alltså att γsd= γSd ?
Förtydligande:
S brukar användas vid laster, som ges i svaret och står för interna krafter
s brukar användas vid koefficienter för stål
Svar: I SS-EN 1990 och A2 definieras γSd som en modellosäkerhetsfaktor för laster och lasteffekter. (Se t.ex. not 4 i tabell A2.4(B) och bilaga C9 i SS-EN 1990. Där anges också att den brukar vara mellan 1 och 1,15.
Om man tittar i den skrift som utgör underlag till detta avsnitt i eurokoden (UIC leaflet 774-1) så finns i princip samma formler där men där används interna krafter, S, i stället för lasteffekter E i uttrycket för Requ och utan denna modellosäkerhetfaktor. Denna faktor kan alltså tolkas som en modellosäkerhet i kopplingen mellan lasteffekten och den interna kraft den ger upphov till. Då lasten i det här fallet är en fiktiv ekvivalent last som uppräknas med ett antal faktorer, där själva beräkningsmodellen för lasteffekten ska ge resultat på säker sida, så borde denna faktor i normala fall kunna sättas till 1
Svar på följdfråga: Det är mycket osannolikt att man i detta fall menar en stålkoefficient eftersom det helt och hållet är fråga om utmattning av själva betongen. Det troliga är att de som redigerat detta inte själva har varit insatta i detta och haft full koll och det därför blivit fel. Denna fråga kommer att föras upp till CEN och det europeiska standardiseringsarbetet (korrigering eller förtydligande) som har ansvar för denna standard,. Tills vidare gäller dock tolkningen att γsd skulle ha varit γSd.
Fråga: Ska faktorn α6 enligt SS EN 1992-1-1, 8.7.3, tabell 8.3, beaktas för tvärkraftsarmering?
Tidigare enligt BBK 04, 6.2.6.2, kunde man skarva alla byglar i samma horisontella snitt. Vid de flesta exponeringsklasser krävdes två mötande C-byglar då 10 mm utökat täckande betongskikt. Men vad gäller nu?
Ekvationen för beräkning av förankringslängd står under rubriken ”Förankring av längsgående stänger” (SS EN 1992-1-1, 8.4). Förankring av byglar finns under rubrik 8.5. I 9.2.2(3) och det står där att omlottskarv för skänkel nära livets yta är godkänd. Huruvida denna skarv kan utföras i samma snitt eller inte är jag osäker på. Hoppas ni kan bringa ordning i begreppen.
Svar: Beräkning av faktorn a6 för skjuvarmering
Det handlar här om skarvning av byglar enligt figur 6.2.6.2e i BBK 04. Andelen ”skarvar i samma snitt” för beräkning av a6 bör då relateras till ett snitt med lutning q enligt fackverksmodellen. Skarvar vars centrum ligger närmare varandra än 0,65 l0 i armeringens riktning anses ligga i samma snitt enligt figur 8.8 i EK2. Skarvar inom avståndet 0,65l0 cotq åt vardera hållet längs balken anses således ligga i samma snitt som en viss skarv, se figur nedan, vilket ger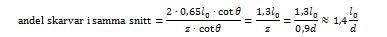
där l0 = skarvlängd, z = inre hävarm, d = effektiv höjd.
Det l0 som bestämmer andelen ska inkludera faktorn a6 vilket kan medföra passningsberäkning.
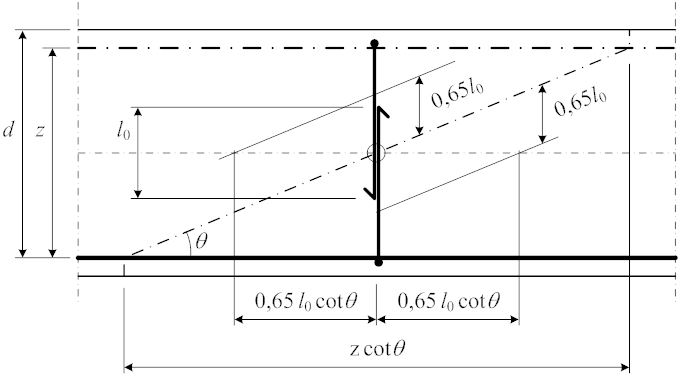
Avsnitt 8.5
Det särskilda avsnittet 8.5 för förankring av byglar ger exempel på godtagbar förankring av bygeländar, vilket kan ses som alternativ till rak förankring med förankringslängd enligt 8.4. Det påverkar därför inte beräkning av skarvlängd vid omlottskarvning av raka stänger enligt ovan.
Avsnitt 9.2.2 (3)
Det som står i 9.2.2 (3) säger bara att det är tillåtet att omlottskarva bygeldelar nära ytan, vilket är vad den första delen av svaret handlar om. Däremot sägs här ingenting om beräkning av skarvlängd med hänsyn till förankring i samma snitt.
Fråga: Jag har en fråga om täckande betongskikt med hänsyn till beständighet i eurokod. I EKS står det att erforderliga åtgärder kan anses ha vidtagits om betongkonstruktionen uppfyller kraven i SS-EN 206-1 och SS 137010 men i eurokoden står det att minsta täckande betongskikt med hänsyn till beständighet för armering enligt SS-EN 10080. Vilken gäller egentligen SS 137010 eller SS-EN 10080?
Gäller den nationella bilagan EKS före?
Svar: För det första så står det i tabellhuvudet att värdena i tabell 4.4N gäller för armering enligt SS-EN 10080, inte att täckskikten ges i standarden.
För det andra så gäller inte tabell 4.4N i Sverige, inte heller tabell 4.5N. De ersätts med de regler för täckskikt som ges i EKS (i tidigare versioner av EKS kanske man hänvisade till SS 137010, men numera står värdena i EKS).
Användning av tabellerna 4.3 - 4.5 är nationellt valbart i eurokoden och vi har i Sverige valt att inte använda oss av dessa. Se anmärkningen till SS-EN 1992-1-1, 4.4.1.2(5).
Fråga: Jag har en fråga angående hur beräkning av vridarmering för betongtvärsnitt behandlas enl SS-EN 1992-1-1? Armeringsbehovet är proportionellt mot Ak och Eurokoden definierar Ak som inneslutning av väggarnas centrumlinjer enl 6.3.2 (1). I BBK 3.8.4 (Armerad betong med vridarmering) definierades Aef som inneslutning mellan hörnstänger i det armerade tvärsnittet. Jag anser det rimligt att välja Ak enl BBK vid beräkning av vridarmering.
Svar: För lådtvärsnitt sammanfaller SS-EN 1992-1-1 och Ak med BBK:s Aef. För massiva tvärsnitt kan Ak sammanfalla med Aef i vissa fall, i andra fall inte. Det är inte säkert att Ak i det senare fallet alltid blir mindre än Aef, det beror på förhållandet mellan A/u och armeringens kantavstånd. Vad som är rimligast kan diskuteras, men skillnaderna torde sällan bli dramatiska. Hur som helst är det SS-EN 1992-1-1 som gäller. Eurokoderna och EKS måste följas. Endast om det saknas delar i eurokoderna eller om en eurokoddel inte införlivats i EKS kan handböcker etc. tillämpas för att verifiera krav på bärförmåga.
Fråga: Jag har en fråga angående minimiarmering i betongplatta på mark för sprickbreddsbegränsning: Som jag tolkar normen så ska man då använda EKV. 7.1 i SS-EN 1992-1-1:2005. I denna formel sätts:
• kc=1,0 (krympning ger ren dragning)
• k =1,0 (gäller för plattor med tjocklek under 300 mm)
• Act sätts till hela betongarean (höjd multiplicerat med 1,0 vid beräkning per meter)
• fct,eff sätts max till fctm (och ej till fctm,fl som presenteras i formel 3.23)
• Finns ett sprickbreddskrav enligt tabell D-2 i EKS sätts ơs till fyk utan till det minsta värde som fås:
- Då man väljer önskad stångdimension i tabell 7.2N pga. sprickbreddskrav (denna stångdimension modifieras sedan i EKV 7.7N)
- Då man väljer önskat stångavstånd i tabell 7.3N pga. sprickbreddskrav
• Finns ej ett sprickbreddskrav (t.ex. en vanlig platta på mark till bostad med föga korrosionskänslig armering i exponeringsklass XC1 och L50) så sätts istället ơs till fyk.
Anledningen till min fråga är att jag tycker att det blir betydligt mer armering i Eurokoden jämfört med gamla BBK. Vill därför kontrollera att beräkningsstegen och värdena ovan stämmer med hur det är tänkt att man ska tolka eurokoden.
Finns det fler reducerande faktorer som man får använda (t.ex. fanns det en teori på BBK:s tid (dock ej omnämnd i normen) som sa att man fick multiplicera den erforderliga armeringsarean med 0,7 om golvet vilade på en yta med låg friktion, t.ex. cellplast)?
Svar: SS-EN 1992-1-1 kan ge mycket minimiarmering, speciellt för tjocka plattor utsatta för rent drag, bl.a. på grund av att man ska räkna med hela tvärsnittsarean, istället för enbart en effektiv area kring armeringen. Frågan har diskuterats i den europeiska tekniska kommittén för bärande konstruktioner av betong (CEN/TC 250/SC 2) sedan flera år tillbaka, men ännu utan resultat.
För mycket tjocka plattor på mark, som utsätts för rent drag på grund av förhindrad krympning, kan detta leda till orimliga armeringsmängder. Minimiarmering behövs dock endast ”vid krav på sprickbreddsbegränsning”, och detta krav behöver ju inte alltid gälla för det inre av en tjock platta. På så sätt skulle man möjligen kunna motivera en minimiarmering baserad på en effektiv betongarea enligt 7.3.2 (3). En sådan tolkning skulle vara sakligt motiverad, med tanke på studier som visar att man verkligen får sprickfördelning inom en effektiv area utan att armeringen dimensioneras för hela tvärsnittsarean. Det strider dock mot definitionen av Act, och är därför formellt tveksamt ur rent formell synpunkt.
Det finns inga fler reducerande faktorer än k och kc.
Kommentar: Observera att formel 7.1 gäller ”om inte en noggrannare beräkning visar att mindre armering är tillräcklig”. Jag hittade ett examensarbete av Robert Edlinger och Karl Svansbo som beskriver en sådan typ av beräkning för en platta med förhindrad krypning, där fuktgradient mm beaktas: Axial- och gradientkrympning hos golv på mark enligt SS-EN 1992 Sprickbredders beroende av betongkvalité, tvångseffekter och armeringshalt.
Fråga I SS-EN 13670 10-6 figur 4 b, finns toleranser för armeringens läge och täckskiktets tjocklek angivna. Där finns en minus tolerans ơdev, som är 10 mm. Den hanteras genom att man i beräkningar lägger på 10 mm, räknar med att täckskiktet kan vara 10 mm tjockare om det är ogynnsamt, och med det nominella täckskitet om det är ogynnsamt. Men sedan finns där en plustolerans, ơplus, på mellan 10 och 15 mm skall den hanteras den? Om konstruktionen är tunn kan ju att flytta in armeringen mot centrum vara mycket ogynnsamt.
Tidigare i BBK fanns en gräns för vid hur tunna konstruktioner ingen särskild hänsyn till toleranser behövde tas vid beräkningar, 150 mm och 250 mm, och vid tunnare behövde armeringen placeras i de ogynnsamaste tänkbara läget toleranserna med gav vid beräkningen. Finns någon sådan gräns även enligt eurokoderna?
Vid beräkning av sprickor till följd av krympning är täckskiktets tjock av betydelse, tjockare är ogynnsammare. Tas på något sätt höjd för den ökning jämfört med det nominella värde som medges i SS-EN 13670 10-6 figur 4b som kan uppkomma, eller måste man vid en sådan beräkning räkna med det tjockaste täckskiktet som toleransen medger? Inte bara lägga på 10 mm för minustoleransen utan även ytterligare 10-15 mm för plustoleransen till den nominella täckskiktstjockleken vid beräkningen.
Det finns även i SS-EN 13670 10-6 figur 4c en tolerans för omlottskarvar. De tillåts vara 6 procent kortare än den angivna skarvlägden.
Är denna toleranser inbakade in det man får då skarvlängden räknas ut enligt eurokoderna, man kan ange den uträknade längden rakt av på en ritning.
Eller måste skarvlängden på ritningar ökas motsvarande toleransen så att den verkliga skarvlängden garanterat inte blir kortare än den beräknade skarvlängden
Svar: Toleranser handlar i första hand om utförandet.
Vid normal dimensionering räknar man således inte med några andra värden än nominella. Det är endast om man i brottgränstillstånd vill utnyttja lägre partialkoefficienter enligt A.2.2 i SS-EN 1992-1-1 som det är aktuellt att räkna med andra värden, som då minskats (i vissa fall ökats) med toleranser. Plustolerans på täckskikt kan i detta sammanhang ses som en minustolerans på effektiv höjd.
Att man räknar med nominella värden är en förutsättning för de partialkoefficienter som man normalt använder (1,15 respektive 1,5). Det gäller även skarvar, där de värden som kan beräknas enligt EKV. 8.7 är nominella. Dessa behöver alltså inte ökas med någon tolerans när de förs in på ritning.
Fråga: Jag försöker använda mig av formeln 7.7N under 7.3.3 - sprickviddsberäkning utan direkt beräkning i SS-EN 1992-1-1:2005.
Jag har tolkat det som att för att utnyttja tabell 7.2N under 7.3.3 så ska en modifierad stångdiameter beräknas. Om förutsättningarna dock skulle vara dem samma som angetts i tabell 7.2N bör den modifierade stångdiametern,
s bli den samma som "största stångdiameter, s vald ur tabell 7.2N. När jag testar att beräkna förutsättningarna givna i tabellen blir det dock väldigt fel. istället för Ø12 blir det Ø7.
Tabellvärdena som jag använder i formel 7.7N från tabell 7.2N är.
Fct,eff = 2,9MPa
hcr= 0,5h
(h-d) = 0,1h 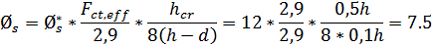
Vad är det för fel? Antar jag fel eller är formeln felaktig?
Följdfråga: Jag var tidigare i kontakt med er gällande problem med beräkning av minimiarmering, dock fick jag inte det svaret jag var ute efter så jag ska förtydliga mig.
Jag fick rådet att räkna med formel 7.6N istället för 7.7N. Men jag har ett fall där det är normalspänningar som påverkar plattan pga krympning, och jag har uppfattat det som att jag då bör använda mig av formel 7.7N.
Men jag förstår inte hur denna modifieringsformel ska appliceras. Jag skulle vilja använda den för att modifiera stångdimensionen i tabell 7.2N då jag inte har samma förutsättningar med betong, täckskikt osv.
Men när jag testar att använda värden givna i tabell 7.2N går det inte ihop. Därför undrar jag nu hur formeln egentligen ska användas. är inte den dragna zonens höjd (hcr) samma i de båda formlerna 7.6N och 7.7N osv. Om jag nu har helt fel, vart är det formeln 7.7N ska appliceras för att modifiera stångdimension?!
Svar: Eftersom hcr = 0,5h så är det uppenbarligen fråga om böjning, inte ren dragning. Då ska EKV. (7.6N) användas, och där ingår kc = 0,4, vilket insatt ger att alla korrektioner blir = 1.
Om det är fråga om dragning (t.ex. p.g.a. förhindrad krympning) så är hcr = h. Resultatet blir då enligt EKV. (7.7N):
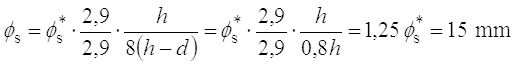
Här är det uppenbarligen fel i formeln. Troligen ska k1 = 0,8 ingå i täljaren eftersom detta värde nämns under tabellen.
Fråga: I SS-EN 1992-1-1 8.7.2 (4) står att ”Då utformningen överensstämmer med (3) ovan får andelen av de dragna stängerna som skarvas i ett snitt vara 100 %, förutsatt att alla stänger ligger i ett lager. Om stängerna placeras i flera lager bör nämnda andel minskas till 50 %. Under (3), vilket det hänvisas till, står att avståndet i längsled mellan två intilliggande omlottskarvar bör inte vara mindre än 0.3 gånger skarvlängden, l0”.
Enligt den texten måste skarvarna förskjutas. D.v.s ett krav motsvarandet det som fanns i BBK 04 3.9.3 (a), vad det gäller att alla stänger inte får skarvas i exakt samma läge och som mest 50 % får skarvas i samma snitt, om än formulerat på ett omständigt sätt. Att 100 % skarvas i ett snitt betyder ju inte nödvändigtvis att de skarvas på samma ställe, så som skarvas i ett snitt är definierat i eurokoderna (att skarvarnas tyngdpunkter hamnar närmare varandra än 1.3 l0.) Speciellt om det är stänger med lite olika skarvlängder blir det lätt en skarv med 100 % i samma snitt.
Det anses stå fel i SS-EN 1992-1-1 8.7.2 (3) och om det är så ska det då tolkas som om skarvarna skall förskjutas 0.3 l0? Om de inte skall förskjutas, vilket då skall vara en mjölighet, finns inget under (3) som påverkar hur skarvarna skall utformas. Det är i sig inget orimligt att inte alla omlottskarvar (av dragen armering) måste vara förskjutna i alla situationer. Att ha det så är ju tex tillåtet i vissa situationer i andra normer. Däremot verkar det inte finnas någon anvisning för i vilka situationer de behöver vara förskjutna eller inte då man tillämpar eurokoderna. Man skulle då alltid få skarva all armering i exakt samma läge, då inget annat sägs. Det verkar inte heller finnas några situationer då omlottskarvning inte får användas alls (om än några det står att omlottskarvning inte bör användas i). Kan man alltid omlottskarva all armering på samma ställe (exakt, inte bara inom samma snitt så som definierat i eurokoderna)?
Är det enda som behöver göras räkna med ett större alfa 6, jämfört med om skarvarna skulle vara förskjutna? Eller finns det delar av eurokoderna, beräkningsmodeller etc som förutsätter att skarvarna är förskjutna och som då inte kan användas?
Vanligt är ju att skarvas anses behöva förskjutas i alla fall i vatten- och gastäta konstruktioner, och andra där man inte kan tillåta stora sprickor, golv tex. Att inte de generalla reglerna för sprickbegränsandearmering inte täcker upp för de påkänningar som blir vid omlottskarvars ändar i alla situationer. Men inget om detta nämns i SS-EN 1992-3, delen om tankar och vattentäta betongkonstruktioner, det enda som finns är ett påpekande under SS-EN 1992-1-1 7.3.3 (4). Och man kan ju tänka sig att mängden tvärgående armering som krävs över en omlottskarv skulle vara bli större om flera intilliggande stänger skarvas på samma ställe, jämfört med att bara en stång skarvas.
Finns det något sagt om när skarvarna bör förskjutas, mer än det väldigt generella under SS-EN 1992-1-1 8.7.2 (2)?
Svar: Avstånd minst 0,3l0 är villkoret för att skarvar ska få anses vara förskjutna, dvs ligga i olika snitt. För skarvar som ligger i samma snitt gäller således alla strecksatser i 8.7.2 (3) utom den om 0,3l0 (kanske lite oklart i 8.7.2).
Man kan inte alltid skarva all armering i samma snitt, endast dragen armering i ett lager (4). Den andel som får skarvas ”i samma snitt” kan dock ligga exakt i samma snitt.
Alla regler som gäller skarvar står i 8.7. Sedan står det ju konstruktören fritt att vara ännu försiktigare i speciella fall.
8.7.2 (4) och andra strecksatsen i 8.7.2 (3) bör inte uppfattas som motstridande, även om en rent ”juridisk” tolkning av texten kan ge det intrycket. En förnuftig tolkning är att 8.7.2 (4) anger under vilka förutsättningar man kan avvika från andra strecksatsen i 8.7.2 (3). Om dessa förutsättningar är uppfyllda kan man skarva alla armering med mindre förskjutning än den som definieras i (3), vilket är vad som åsyftas med ”i samma snitt” i den svenska översättningen.
Fråga: Jag har en fråga angående förankringslängd av armering, i SS-EN 1992-1-1:2005 avsnitt 8.4. Vid val av α4 i Tabell 8.2, gäller värdet 0,7 alltid? Det verkar väldigt märkligt att reducera med 0,7 om det inte finns någon omslutning av fastsvetsad tvärarmering som α4 är faktor för. Ska man istället välja 1,0 om man inte har någon omslutning av fastsvetsad tvärarmering?
Svar: a4 = 0,7 gäller om det finns påsvetsad tvärarmering som uppfyller villkoren i figur 8.1e, om inte så är a4 = 1,0.
Fråga: I SS-EN 1992-3 kap 7.3.1 anges som krav för vattentäthet att genomgående sprickor ska begränsas eller i allmänhet undvikas.
Svar:
För Trafikverkets byggnadsverk regleras användningen av SS-EN1992-3 i TRVK Bro 11, D.2.2.1.3.
Fråga: I EKS 3.2.2(3)P 9a § står att Armering med sträckgräns, 500 < fyk ≤ 600 MPa får användas om relativ kamarea fr ≥ 0.11.
Vad är det för armering som uppfyller det kravet på relativ kamarea (naturligtivs ihop med övriga krav som måste uppfyllas för att armeringen skall få användas enligt EKS)?
Hur beskriver man den lämpligen tex på en föreskriftsritning eller vid beställning?
Svar: Värdena på fR i tabell C.2N är nationellt valbara, och regeln i EKS innebär att kravet höjs för armering med fyk ≥ 500 MPa. Mig veterligt uppfylls detta krav av den armering B500B från Celsa som vanligen används i Sverige. Däremot kan man inte vara säker på att detta gäller för annan armering, t.ex. importerad utanför Skandinavien.
För armering med fyk < 500 MPa gäller rekommenderade värden.
På en föreskriftsritning eller i en beställning bör man med anledning av denna skärpning, vars bakgrund jag inte känner till, förutom övriga krav på armeringen även ange krav på relativ kamarea fR.
Föreskriften 3.2.2(3) P är överflyttad från BKR och är baserad på äldre forskningsrön.
Fråga: Jag vore mycket tacksam för hjälp med en fråga ang tolkning av SS-EN-1992-1-1 avsnitt 9.8.2 angående armering i grundplattor:
I vanliga grundplattor/pelarfundament (typiskt en centrisk pelare med huvudsakligen vertikal last på en rektangulär platta med liten utsträckning, säg storleksordning 3 x 3 m) behövs ofta endast en underkantsarmering för bärförmågan (vid momentbelastning i pelaren kan även en liten mängd överkantsarmering erfordras).
Då övriga lasteffekter såsom tvångsspänningar av förhindrad krympning och temperaturrörelse är små (pga plattans begränsade utbredning), så att den totala dragspänningen i överytan i bruksgränstillstånd blir mindre än draghållfastheten, och överytan därmed kan anses osprucken, kan jag inte se att någon speciell minimiarmering behöver inläggas i överytan (utöver den som eventuellt behövs för brottgränstillstånd).
Jag tolkar skrivningen i SS-EN 1992-1-1 avsnitt 9.8.2 för grundplattor:
som en bekräftelse på mitt resonemang ovan, d v s att armering endast behöver inläggas om så erfordras med hänsyn till bärförmåga i brottgränsttilsstånd, eller om plattan kan förväntas spricka i bruksgränstillsstånd (och man behöver begränsa sprickvidden). Om så inte är fallet behövs ingen armering (d v s för en grundplatta finns inga andra speciella minimiarmeringskrav).
Är denna tolkning riktig?
Svar: De dragspänningar som uppstår i överytan på en grundplatta är ju i regel inte nödvändiga för jämvikten i brottgränstillstånd, utan en sekundär effekt av att trycksträvan i en fackverksmodell till stor del passerar långt från överkanten. Om man vill begränsa sprickbredder bör minimiarmering enligt 7.3.2 läggas in, men i regel finns väl knappast behov av att begränsa sprickbredder i överkanten på en grundplatta, om där inte finns någon armering med statisk funktion (såsom i en grundplatta med i huvudsak centrisk last).
För en grundplatta med excentrisk last blir det annorlunda, då kan ju uppstå dragkrafter i överkanten som måste tas av armering, men det är ju en annan fråga.
Fråga: Finns information tillgänglig från de utredningar vari man tagit fram parametrarna för exempelvis explosiv spjälkning? Vart kan man i så fall ta del av dem? I SS-EN 1992-1-2 kapitel 6.2 står som metod d att 2 kg per kubikmeter är det minsta tillåtna värde för addering av polypropylenfiber men jag kan emellertid inte hitta någon bakomliggande förklaring eller data till det valda värdet.
Svar: Tyvärr är ofta källhänvisningen i Eurokoderna generellt ganska bristfällig. Bakomliggande orsak till inblandning av polypropylenfibrer känns säkert till. Det är ju framförallt vid högpresteande betong som är tät och med hög hållfasthet som stora inre tryck kan uppstå och leda till explosiv spjälklning. Syftet med polypropylenfibrer är ju att dessa ska smälta vid uppvärmningen och därmed en mer porös struktur erhålls som gör att ångtrycket kan minska. Hur man just kommit fram till siffran 2 % vet jag däremot inte men troligen finns det vissa försök bakom denna.
Fråga: Hur ska SS-EN 1992-1-1 kapitel 9.2.1.4 & 5 beaktas för en spännarmerad balk?
- Gäller dom inte?
- Gäller dom endast för slakarmering?
- Gäller dom för totalt armeringsinnehåll, inkl. spännarmering?
Svar: 9.2.1.4 (1) gäller i princip, men lär inte vara något problem för en spännarmerad balk, eftersom spännarmeringen i regel går oavkortad till ändstöd.
9.2.1.4 (2) är knappast heller något problem för en balk med efterspänd armering, eftersom armeringen är ändförankrad vid änden. Vid förespänd armering med vidhäftningsförankring måste dock denna regel beaktas, och för förankringen av kraft enligt EKV. (9.3) gäller då även 8.10.2.3. Regeln handlar om att man ska kunna förankra en viss kraft i brottgränstillstånd, påverkad av tvärkraft, och då kan man räkna med både slak och spänd armering.
9.2.1.5 (1) hänvisar till 9.2.1.4 (1), se därför ovan.
9.2.1.5 (2) och (3) kan tillämpas för underkantsarmeringen i en platsgjuten efterspänd balk. För prefab är det svårare, om man vill göra en förespänd balk kontinuerlig. Här måste man i vissa fall kunna göra undantag, som t.ex. för TT-kassetter, som görs kontinuerliga över mellanstöd med slakarmering i överkanten. Här finns ingen praktisk möjlighet att ordna en sammanbindande underkantsarmering.
Fråga: Jag dimensionerar ett flertal plintar som uppfyller de geometriska villkoren för full diskontinuitet enligt 6.5.3 (3). När jag räknar ut dragkraften T enligt EKV. (6.58) och (6.59) så får jag ändå ett större värde på dragkraften med EKV. (6.58). I vissa fall så får jag till och med ett negativt värde med EKV.. (6.59). Det här verkar bero på att vi har ganska låga plintar och stora fotplåtar. Ett exempel på en sådan geometri är en plint där höjden H = 1,60 m, plintsidans längd b = 2,0 och fotplåtens sida är a = 0,85m. Lasten är 14,7 MN. Ekvationen för partiell diskontinuitet ger T = 2113 kN och ekvationen för full diskontinuitet ger T = 942 kN. Vilket värde på dragkraften är rätt?
Svar: EKV. (6.59) är troligen fel, det bör vara H istället för h. Om (6.59) ändå skulle ge lägre värde än (6.58) bör den senare användas. Felet uppmärksammades för flera år sedan, men jag vet inte om det kommit med i någon rättelselista.
Fråga: Jag har en fråga om prägling. Är det korrekt att vid prägling under lokalt tryck där lasten kan sprida sig i enbart en riktning begränsas kapaciteten till roten ur tre fct istället för tre fct. Är det så man ska uppfatta punkt 6.7 i SS-EN 1992-1 (med tillhörande figur 6.29). Tidigare, i BBK 04, fanns inte begränsningen att b2<3*b1 och d2<3*d1.
Svar: En kraft som står vid en kant och är riktad längs kanten ger ingen förstoring alls. Det följer av definitionen av fördelningsytan Ac1 som likformig med tryckytan Ac0 och med tyngdpunkten på kraftens verkningslinje. För att det ska kunna bli någon förstoring, d.v.s. fördelningsytan bli större än tryckytan, måste kraften luta inåt, så att verkningslinjen avlägsnar sig från kanten.
Fråga: Vi har noterat att viss kommersiellt tillgänglig mjukvara misstolkat begränsningarna för Ac,eff på så sätt att de tolkar begränsningarna som generella för all utformning och inte specifikt för respektive delfigur såsom texten med sin förtydligande parantes anger. Följden av denna feltolkning blir i många fall att armeringen är placerad utanför Ac,eff.
Vi vill be er att bekräfta att detta är en olyckligt otydlig formulering och att den även fortsatt ska läsas såsom den läses t.ex. i BBK eller DIN?
Samma figurer återfinns i BBK94 på ett mycket tydligt sätt samt i BBK04 där rättelsebreven korrigerar liknande vantolkningar enligt ovan.
(Se även bifogad fil för förtydligande)
Svar: De tre begränsningarna 2,5(h-d), (h-x)/3 och h/2 gäller inte specifikt för delfigurerna a), b) respektive c). De gäller generellt för alla olika fall, med undantag för att (h-x)/3 helt enkelt inte är relevant för c), då det där saknas tryckzon.
Boverket kan inte se några större svårigheter med att tolka de tre figurerna eller hur Ac,eff ska bestämmas. Om den programvara som används inte räknar rätt bör annan programvara användas eller handberäkningar göras.
Fråga: Kontroll av nödvändig förankringslängd för armering finns redovisat i SS-EN 1992-1-1 kap.8. Här anges i punkt 8.1 att detta kapitel endast gäller kamstänger, vilket är det normala i dag men hur gör man om man måste kontrollera en slät stångs förankring både med och utan ändbock/slinga? Tidigare fanns det en generell formell i Betonghandboken som gällde både för kamstång och slätstång kap 3.9:123.
Svar: Dimensioneringsreglerna i SS-EN 1992 gäller enbart för kamstänger, eller andra stänger (t.ex. profilerade) som uppfyller kriterierna för relativ kamarea i bilaga C. Det finns således inga regler för släta stänger. Vad man kan göra, t.ex. vid kontrollberäkning av en befintlig konstruktion med släta stänger, är att tillämpa reglerna i BBK 04. Betonghandboken ger såvitt jag vet inget utöver BBK när det gäller släta stänger.
Om frågan gäller ett befintligt byggnadsverk ska de regler som gällde när byggnaden uppfördes tillämpas. Andra armeringsstänger än kamstänger eller profilerade stänger med en angiven relativ kamarea får inte användas i lastbärande konstruktioner där armeringen har betydelse för bärförmågan.
Fråga: Vi armerar balkongplattor som är inspända i bakkant. Kap 9.3.1.4 Armering fri kant säger att vid fri kant bör en platta normalt vara försedd med längsgående och tvärgående armering enligt figur 9.8. Vilket minimiavstånd c/c behövs på C-byglarna?
Om man går i n i kap 9.3.2 Tvärkraftsarmering och försöker tolka så säger flera saker emot varandra. Plattorna bör vara minst 200 mm tjocka och man ska då lägga skänklarna på c/c 1,5d. När det gäller balkongplattor, så understiger framkanten i princip alltid 200 mm, speciellt om uthänget inte är så stort. Gäller 1,5d fortfarande då man är under 200 mm?
Byglarna börjar bli väldigt små och täta. Följer man kap 9.2.2 för tvärkraftsarmering så hamnar man ännu tätare (0,75d). Gjuteriet som ska gjuta plattorna undrar varför jag lagt byglarna så tätt. De har tidigare aldrig ens haft byglar på liknande balkongplattor räknade enligt gamla normer.
Svar: Eftersom ingenting sägs om byglarnas mängd och avstånd så tycker jag att man normalt kan se dem som en ren monteringsarmering. Då blir det en praktisk fråga om hur de bör utformas, och jag tycker inte att man ska behöva tillämpa regler för skjuvarmering, eftersom byglarna sällan har denna funktion. Det kan naturligtvis finnas fall där man behöver utnyttja vridmoment eller stor tvärkraft längs en fri kant, och då kan dimensioneringen ge krav på byglarna, men detta är nog sällan fallet i en balkong.
Fråga: Jag har en fråga gällande minimikrav på tvärarmering för balkar och pelare där det i vissa fall verkar krävas dubbla byglar.
Kap 9.2.2 (8) konstaterar att "Avståndet i tvärled mellan tvärkraftsarmeringens skänklar bör inte överstiga st,max=75d <=600 mm". Innebär det att om man exempelvis har en rektangulär balk eller en balk där skillnad mellan höjd och bredd är liten så måste man lägga in dubbla byglar? Som exempel kan tas en balk som är 200 x 200 mm som armeras med 3 ø 12 i uk. Vid täckskikt för förankring (ø + 10 mm) blir avståndet mellan skänklarna större än 0,75d, och då måste man enligt EC lägga in dubbla byglar med utformning av typ figur 9.5.
Liknande problem finns för pelare. I kapitel 9.5.3 (6) står det att"[...]Ingen stång inom tryckt tvärsnittsdel bör placeras på större avstånd än 150 mm från en stång omsluten av ett bygelhörn eller annan likvärdig omslutning." Detta skulle för en pelare med måtten 200 x 600 mm som armeras med stående 3+3 ø 20 alltså innebära att dubbla byglar måste läggas in som förbinder stängerna 4 och 4 så att avståndet till ett bygelhörn aldrig är längre än 150 mm?
Svar: En balk på 200 x 200 mm kan nog betraktas som en ”bärverksdel av mindre betydelse”, och i så fall behövs ingen minimiskjuvarmering. Om en sådan balk skulle behöva beräkningsmässig skjuvarmering så skulle den enligt kap 9.2.2 (8) behöva ha flera skänklar än två. För en större balk, som inte är ”av mindre betydelse”, gäller detta oavsett om det är minimiarmering eller beräknad armering.
Detta kan verka lite onödigt för en kvadratisk balk ”av mindre betydelse”, och själv tycker jag att det i så fall borde räcka med två skänklar, men det kan vara svårt att dra gränsen mot balkar ”av större betydelse”.
När det gäller pelare så är bakgrunden att byglarna ska förhindra utknäckning av tryckta stänger. I exemplet skulle man kunna ändra armeringsutformningen så att ingen stång hamnar längre än 150 mm från en omsluten stång, eller också kan man dela upp byglarna så att varje bygel bara omsluter 4 stänger.
Fråga: Har en fråga angående "sprickbreddsbegränsning utan direkt beräkning" och hur tabellerna 7.2N och 7.3N ska användas?
Svar: Man måste först beräkna en armeringsspänning för sprucket tvärsnitt. Sedan går man in i respektive tabell och avläser största stångdiameter för en viss sprickbredd (tabell 7.2N, mest lämpad för balkar o.d.) respektive största stångavstånd (tabell 7.3N, mest lämpad för plattor o.d.). Vid behov görs korrigeringar enligt text i anslutning till tabellerna. Man ska komma ihåg att tabellerna kan ge mycket konservativa resultat, och att en sprickbreddsberäkning enligt 7.3.4 ofta lönar sig.
Fråga: I BBK 04 kap 6.2.6.2 fanns krav på maxavstånd för byglar (s300) för balkar i brandteknisk klass R30 eller högre. Hur är det i Eurokoden, har detta krav slopats? Har sökt i SS-EN 1992 och delen för brand samt handböckerna till eurokoder men hittar inget motsvarande krav.
Svar: I brandavsnittet i Eurokoden finns inga specifika krav på bygelarmering av balkar utan de krav som finns vid brottlastdimensionering kan förutsättas vara tillfyllest även vid lastfallet brand.
Fråga: Jag hittade ett dokument på er hemsida vid namn "Utmattningsdimensionering av betongbroar enligt Eurokod" där Elisabeth Helsing står som författare. Jag har en fråga angående lambda-metoden enligt SS-EN 1992-2, Bilaga NN.
När lambda (2-4) ska räknas ut så finns en faktor k2 med. Som förklaring till k2 står "lutningen på tillämplig Wöhlerkurva".
Min fråga är om det alltid ska vara k2 eller ska det egentligen stå ki där (i=1 eller 2). Det vill säga om jag har ett mindre värde på Nobs än N* på Wöhlerkurvan så skulle det då bli k1 där istället.
Svar: Vi har studerat denna fråga förut och kommit fram till att för den här tillämpningen ska k2 användas konsekvent.
Fråga: I kapitel 6.8.1 står det angående utmattningsverifiering att detta i allmänhet inte är nödvändigt för t.ex. grundkonstruktioner. Vilka konstruktionstyper innefattas av begreppet grundkonstruktioner? Hittar ingen definition av detta i eurokoden. Är t. ex en bankpålplatta och ett påldäck att betrakta som grundkonstruktioner?
Svar: Den avgörande regeln är första raden i (102): ”Utmattningsverifiering bör utföras för bärverk och bärverksdelar som utsätts för regelbundna lastväxlingar.” Anmärkningen är av handbokskaraktär. De undantag som står i anmärkningen upplyser bara om att utmattningskontroll i allmänhet inte är nödvändig för vissa bärverksdelar. Vad som är avgörande för om en utmattningskontroll behövs i ett enskilt fall är storleken på lastväxlingarna. Om en utmattningskontroll behövs måste alltså alltid bestämmas i det enskilda fallet. Frågan om definition av begreppet grundkonstruktion faller därmed.
Fråga: Vi skriver anvisningar hur bergförstärkning skall utföras och har tidigare hänvisat till BBK 04 för dimensionering med partialkoefficienter för att erhålla dimensionerande värden och undrar vilken Eurokod som idag är korrekt att hänvisa till?
Svar: Partialkoefficienter för dimensionering av armeringsstål hittar man i SS-EN 1990 och SS-EN 1992-1-1.
Observera att bergkonstruktioner under mark inte ingår i Eurokoderna. De beräkningsmodeller för dimensionering med säkerhetsindex och matematiska modeller för konstruktioners tillförlitlighet som är grunden för eurokods säkerhetsformat är dock att betrakta som matematiskt allmängods.
De säkerhetsnivåer som Boverket beslutat om, och som gäller för de byggnadsverk som Boverkets regler gäller för, finns publicerade i EKS, Boverkets föreskrifter och allmänna råd om tillämpning av europeiska konstruktionsstandarder (eurokoder)
https://rinfo.boverket.se/EKS/PDF/BFS-2013-10-EKS-9.pdf. Förstärkning av berg är inget som omfattas av dessa regler men modellen med partialkoefficienter kan tillämpas även för andra områden. De brottsannolikheter som eftersträvas i EKS är en formell årlig brottsannolikhet på 1/10 000 för säkerhetsklass 1, 1/ 100 000 för säkerhetsklass 2 och 1/1000 000 för säkerhetsklass 3. Den faktiska sannolikheten är förmodligen betydligt lägre i de allra flesta fall.
Fråga: Jag har en tolkningsfråga gällande Eurokoden för betong, enligt ämnesraden. Hoppas att jag nu skickar till rätt e-postadress. Vidarebefordra annars gärna. Frågan gäller specifikt fallet där man maximerar en gjutfogs c och µ med hjälp av förtagningar (Kap. 6.2.5(2), figur 6.9).
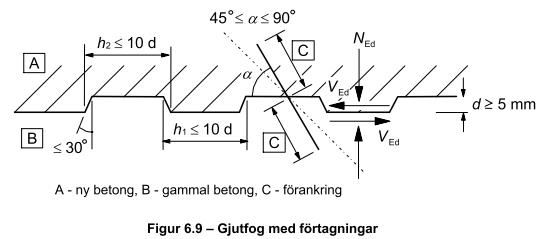
I figuren kan man utläsa ett minimivärde för förtagningarnas djup och ett maxvärde för deras längd. Men det finns inga minimivärden för förtagningarnas längd (h1 och h2) och inte heller någon begränsning i hur stor skillnad det får vara mellan dem (h1 och h2). Detta innebär som jag tolkar det att man skulle kunna göra slitsar i en stående vägg-fog, säg 15 x 15 mm med ett c/c-avstånd på 150 mm och uppnå samma c och µ som om man gjorde 15 mm förtagningar jämnt fördelat (h1 = h2 = 150 mm). Rent intuitivt går dock inte detta ihop för mig, då den senare varianten i min värld borde ha betydligt större kapacitet att föra över tvärkrafter.
Är detta en fråga som har varit uppe tidigare? Har jag missat något? Borde det ha funnits ett minimivärde för både längd och diskrepans mellan h1 och h2?
Svar: Det är säkert bättre med fler och kortare förtagningar. Regeln är dock inte tillräckligt nyanserad för att ta hänsyn till detta. Man har valt en enkel variant där man enbart ställer upp geometriska minimikrav. Man kan jämföra med förankring av armering, där beräknad vidhäftning förutsätter att armeringen uppfyller vissa minimikrav på relativ kam-area. Det ges för närvarande ingen möjlighet att tillgodoräkna sig högre värden på relativa kam-arean (den armering som används i Sverige har ofta betydligt högre värden).
Fråga: Jag har en fråga angående beräkning av förskjutning av dragkraftskurvan vid förkortning av armering.
När den förskjutna dragkraftskurvan beräknas enligt kapitel 9.2.1.3 (2) så beräknas vid vertikala byglar den sträcka al som kurvan förskjuts z·cot(θ)/2 enligt ekvation 9.2. Genom att använda ekvation 9.3 i 9.2.1.4 (2) och skriva om den så kan man teckna förskjutningssträckan al i termer av relationen mellan krafttillskott och tvärkraft multiplicerat med inre hävarm. I fall av ingen verkande normalkraft blir ekvation 9.3 al = (Fed/|VEd|) ∙z.
Om man låter vinkeln på trycksträvan vara svävande mellan gränsvärdena 1,0 ≤ cot(θ) ≤ 2,5 så kan man genom att uttrycka antal byglar som behövs för att klara tvärkraft (n) som n=VEd/(fywd∙ Asw) och använda delningsmått s för att beräkna sträcka, teckna tan(θ)=z/(s ∙ n)=(0,9d ∙ fywd ∙ Asw )/(s ∙ VEd). Om man skriver om ekvation 6.8 i 6.2.3 (3) och bryter ut cot(θ) så kan man på samma sätt teckna vinkeln på trycksträvan i termer av hur många byglar som strävan korsar och vad varje bygel klarar.
Horisontellt dragkraftstillskott kan om det skrivs som ΔFed = VEd/(2 ∙ tan(θ)) användas för att teckna förskjutningssträckan al i varje given punkt längs balken så att förskjutningsländen relateras till hur kraftsituationen ser ut i varje punkt och inte relateras till ett fast värde på cot(θ) enligt:
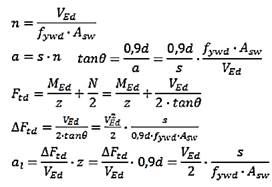
På de ställen i balken som utsätts för dimensionerande tvärkraft så blir förskjutningssträckan beräknad med det cot(θ)-värde som antagits vid tvärkraftsberäkningen, men i de snitt där tvärkraften är mindre blir den teoretiska lutningen på trycksträvan brantare.
Är detta ett acceptabelt beräkningssätt eller måste cot(θ) sättas till det fasta värde som antagits vid tvärkraftsberäkningen?
Vad jag kan se leder den brantare trycksträve-vinkeln på ställen med mindre tvärkraft aldrig till att tvärkraftskapaciteten för balken överskrids. Dock är antagandet att balken fungerar som ett fackverk teoretisk, så det är oklart hur långt man kan sträcka logiska resonemang. En förtydligande rekommendation angående detta vore önskvärd.
Svar: Dragkraftsökning p.g.a. tvärkraft kan för balkar med skjuvarmering beräknas ur jämviktsvillkor i fackverksmodellen. Resultatet kan uttryckas antingen som dagkraftsförförskjutning eller krafttillskott. Krafttillskott ges av ekvation 6.18 och dragkraftsförskjutning av ekvation 9.2. Dessa ekvationer uttrycker i princip samma sak. För balkar utan skjuvarmering finns endast möjligheten dragkraftsförskjutning, som i SS-EN 1992 sätts = d (1,5d i BBK).
Cot(θ) kan det för en given skjuvarmering i ett givet snitt sättas till det värde som ger tillräckligt antal byglar för att bära tvärkraften. Detta cot(θ) kan då vara mindre än det värde som använts vid dimensionering av skjuvarmeringen, om byglarna är lite överdimensionerade, vilket de ju lätt blir i vissa snitt när man väljer konstant delning inom vissa delområden.
Frågor: Böjarmering vid kantpelare och innerpelare:
Böjarmeringsinnehåll vid genomstansning; enligt kapitel 9.4.2 (1) står det att böjarmeringen vid kant- och hörnpelare fördelas på sträckan .
Hur mycket av den böjarmering som löper parallellt med kanten vid en kantpelare får man räkna med? Hur mycket av böjarmeringen intill innerpelare får man räkna med?
Lokalt tryck:
Enligt kapitel 6.7 ska "" vara likformig med "" och tyngdpunkten för "" bör ligga på kraftens verkningslinje.
Hur blir det i så fall när t ex en kantpelare står kant i kant med bjälklaget? Blir fördelningsytan "" samma som den belastade arean ""?
Skjuvarmering vid stansning:
Det står i kapitel 6.4.5 (4) att kontrollsnittet bör beräknas enligt ekvation 6.54 och att skjuvarmeringen sedan inte bör placeras längre innanför än avståndet kd.
Hur bestämmer man avståndet från belastad area till kontrollsnittet ? Ska man först prova sig fram med armering och sedan beräkna ett kontrollsnitt utifrån den armeringen?
Svar: Böjarmering vid kantpelare och innerpelare:
För armering som ska ta moment vinkelrätt mot kanten finns uppgifter, men för armering längs kanten liksom för innerpelare sägs ingenting i kapitel 9.4.2. Man kan tillämpa bilaga I, enligt vilken man för innerpelare räknar med en "pelarstrimla" med bredden ly/2 (se figur I.1). För en kantpelare kan man analogt räkna med bredden ly/4. Smärre avvikelser ifråga om fördelningen mellan pelarstrimla och mittstrimla bör också kunna accepteras. Det viktiga är att totaljämvikten beaktas.
Hur man väljer att fördela momenten och därmed armeringen, dels mellan stöd och fält, dels mellan pelarstrimla och mittstrimla, har också betydelse för bärförmågan för genomstansning. De gränser som rekommenderas i tabell I.1 ger ganska stor frihet.
Lokalt tryck:
För en kraft vars tryckyta ligger kant i kant med den belastade konstruktionen, och som inte lutar i förhållande till kanten, blir det mycket riktigt ingen förstoring av tryckhållfastheten. Anledningen är att det då inte finns förutsättningar för något treaxligt tryck. Om kraften lutar inåt i den belastade konstruktionen kan däremot fördelningsytan bli större än tryckytan, och då kan det bli förstoring.
Skjuvarmering vid stansning:
Nödvändig längd på kontrollsnittet för tillräcklig bärförmåga utan skjuvarmering, uout respektive uout,ef, kan beräknas "baklänges" med hjälp av ekvation 6.38 och 6.47 och lösningen är ekvation 6.54. Att sedan utifrån denna längd bestämma avståndet från belastad area är ett geometriskt problem som möjligen fordrar en iteration när det gäller uout,ef.
Fråga: I kapitel 3.1.5 och 3.1.7 anges arbetskurvor för betong. Hur ska kontroller enligt kapitel 7 SLS betraktas? Är det en tvärsnittsdimensionering enligt kapitel 3.1.7 eller ska ett mer realistiskt beteende enligt kapitel 3.1.5 användas?
Svar: Tvärsnittsdimensionering enligt kapitel 3.1.7 avser (underförstått, om än inte klart utsagt) brottgränstillstånd och är inte aktuellt i bruksgränstillstånd. Om man vill göra en noggrann beräkning (icke-linjär) i bruksgränstillstånd kan man använda arbetskurva enligt kapitel 3.1.5, men normalt nöjer man sig med att anta linjärt beteende och då behöver man bara E-modulen.
Fråga: Jag har ett par funderingar som rör minimiarmering enligt Eurokoden.
Minimiarmering enligt kapitel 7.3.2
Ekvation 7.1 ger för tjocka konstruktioner väldigt mycket armering. Frågan har ställts på er hemsida hur detta ska hanteras, följande två svar finns att läsa (det första högre upp på sidan och det andra längre ned):

samt:

Svaren är som synes motstridiga, där det första säger att en effektiv betongarea "borde kunna användas", det andra att hela den dragna betongarean ska medräknas. Vad är det som gäller?
Vidare funderar jag på vilken stålspänning som ska användas i ekvation 7.1 då det finns sprickviddskrav. Stålspänningen ska enligt kapitel 7.3.2(2) reduceras vid krav på sprickbreddsbegränsning. Följande står att läsa på FAQ-sidan:

Det står även i Eurokoden:
Av detta tolkar jag det som att jag beroende på sprickviddskrav och stångdimension kan välja en stålspänning i tabell 7.2N och använda mig av i formel 7.1. Denna stålspänning borde ge en konservativ armeringsmängd och därmed vara på säkra sidan.
Jag har dock fått olika svar gällande denna metod och undrar vad som gäller?
Minimiarmering enligt kapitel 9.2.1.1
Denna minimiarmering är till för att konstruktionen ska vara robust och klara tvärsnittets sprickmoment. Följande svar finns att läsa på FAQ-sidan:

Om konstruktionen beräknas för olika lastfall (burks-, brott- och olyckslastfall), har man då inte tagit hänsyn till alla laster? Det borde därmed inte kunna ske "en plötslig kollaps" eftersom konstruktionen har armerats för att segt brott ska uppstå.
Armering enligt kapitel 9.2.1.1 blir ibland för tjocka konstruktioner dimensionerande (ger ibland dubbelt så mycket armering än vad som krävs i de olika lastfallen). Går det att motivera bort denna med hänsyn till att samtliga lastfall beräknats?
Krävs denna minimiarmering även i snitt som är obelastade, eller gäller den endast för snitt utsatta för dragspänningar?
Svar: Att de två första citerade svaren låter lite olika torde bero på att de tillkommit vid olika tidpunkter. Efter det första svaret gjordes en del studier som tydde på att effektiv betongarea enligt SS-EN 1992, trots att den är större än BBK:s, kunde ge för lite armering i mycket tjocka tvärsnitt. Frågan har också diskuterats (och diskuteras fortfarande) inom SIS/TK 556 inför kommande revideringar av SS-EN 1992. Tillsvidare finns ingen officiellt sanktionerad möjlighet till avsteg, men det som står i första stycket i det första svaret bör kunna beaktas.
Beträffande användning av tabell 7.2N eller 7.3N så är det alltid ett accepterat alternativ, även om det kan ge konservativa resultat. Vad som sagts och skrivits i olika sammanhang är att en beräkning av sprickbredd ofta ger gynnsammare resultat än tabellerna. För att beräkna en armeringsspänning att sätta in i ekvation 7.1 skulle man då kunna använda ekvation 7.9 och 7.11 "baklänges" utifrån ett visst sprickbreddskrav.
Trafikverket har sina speciella krav när det gäller broar. Således fordras att sprickbredder beräknas enligt kapitel 7.3.4, tabellmetoden i 7.3.3 är inte accepterad. (Motsvarande gäller deformationer, som ska beräknas enligt kapitel 7.4.3 och inte verifieras med hjälp av tabellmetoden i 7.4.2.)
Slutligen minsta böjarmering enligt kapitel 9.2.1.1: Denna armering har bl.a. till uppgift att förhindra plötsliga (spröda) brott. Det innebär att armeringen måste kunna klara minst den last som gör att betongen spricker, annars blir det ett plötsligt brott när denna last uppnås. Det kan i vissa fall innebära att armeringen klarar en last som är större än vad som krävs i aktuella gränstillstånd. Att enbart dimensionera armeringen för aktuella laster och gränstillstånd är dock i sig ingen garanti för ett segt brott, och man kan därför inte "motivera bort" minimiarmeringen med hänvisning till övrig dimensionering. Enda sättet att komma ifrån kravet på minimiarmering är att dimensionera konstruktionen som oarmerad enligt kapitel 12, men det är väl sällan aktuellt för en balk eller platta.
Fråga: Var i Eurokoden kan man hitta dimensioneringsregler då man ska gjuta vattentäta konstruktioner under grundvattenyta?
Svar: SS-EN 1992-3 kapitel 7 behandlar vattentäthet i behållare och liknande konstruktioner. Detta bör kunna tillämpas även för grundkonstruktioner under grundvattenytan som ska vara täta.
Fråga: Ekvation 8.5 är en begränsning av produkten α2, α3 och α5 som gäller för beräkning av förankringslängd enligt Kap 8.4.4
Vid beräkning av skarvlängd enligt Kap 8.7.3 (1) hänvisas till Tabell 8.2. Men gäller begränsningen enligt EKV 8.5 även i skarvlängdsfallet?
Svar: Huruvida EKV (8.5) ska gälla även vid skarvning är oklart.
I 8.7.3 (1) står att α1, α2, α3 och α5 bestäms enligt Tabell 8.2. Faktorerna beskrivs i 8.4.4 (1), tillsammans med begränsningen enligt ekvation (8.5). Man kan då tolka det som att beskrivningen inklusive ekvation (8.5) gäller även vid skarvning. En annan tolkning är att hänvisningen i Kap 8.7.3 endast gäller tabell 8.2, inte det övriga som står i 8.4.4 (1), d.v.s. inte EKV (8.5).
Frågan bör avgöras av berörd myndighet.
Eftersom det bara hänvisas till Tabell 8.2 och inte till avsnitt 8.4.4(1) borde inte uttrycket (8.5) gälla för tillämpningen enligt 8.7.3(1) . Hade motsvarande stått i t.ex. en tabellnot hade slutsatsen blivit en annan. En annan sak som talar mot tillämpning av uttryck (8.5) är att α3 är något modifierad.
Det är dock inte möjligt att utan en noggrannare utredning avgöra vad som gäller. För att kunna göra det behöver frågan tas upp med CEN, Europrean Committee for Standardization.
Fråga: Jag har en fråga angående sprickbildning enligt SS-EN 1992-1-1 avsnitt 7.3.3 (5).
Kan punkten tolkas så att om kraven enligt avsnitt 9.2.2, 9.2.3 samt 9.2.4 uppfylls så behöver ingen kontroll av skjuvspricksbredder kontrolleras och fywd=fy kan väljas för beräkning av skjuv- och vridarmering?
Svar: Det är rätt tolkat att om minimiarmering enligt dessa avsnitt i avsnitt 9 läggs in avseende skjuvarmering och vridarmering, så behöver sprickbredder från skjuv- och vrideffekter normalt inte kontrolleras. Dimensionerande skjuvarmeringshållfasthet fywd ska väljas för dimensionering i brottgränstillståndet (inte bruksgräns) enligt avsnitt 6. Observera att effektiv fywd i vissa fall kan vara lägre än fyd.
Det ovanstående är en formell tolkning av texten i SS-EN 1992, avsnitt 7.3.3 (5). Om man verkligen vill vara säker på att ett visst sprickbreddskrav uppfylls är det inte säkert att minimiarmering räcker, eftersom minsta skjuvarmering enligt avsnitt 9.2.3 grundar sig på utnyttjande av skjuvarmeringens flytgräns fyk. Det kan då vara lämpligt att dimensionera/kontrollera skjuv- och vridarmering även med hänsyn till sprickbredd.
Noggrann beräkning av skjuvsprickor i bruksgränstillstånd behandlas t.ex. i Betongföreningens Handbok till SS-EN 1992, Betongrapport 15, utgåva 2, 2012. Ett enklare sätt kan vara att grunda minimiarmeringen enligt avsnitt 9.2.3 på en lägre spänning än fyk, t.ex. enligt avsnitt 7.3.3.
Fråga: Det råder en viss förvirring när det gäller när betong spricker enligt SS-EN 1992 åtminstone i Sverige. I normen gäller generellt att sprickkriteriet är fctm eller fctm,fl om sektionen endast är utsatt för böjning. Sedan finns det i svenska annexet kriteriet fctk/ksi där ksi beror av miljö och livslängdsklass. Frågan är vilket som skall användas? I Betongföreningens handbok SS-EN 1992 volym I avsnitt 7.1 kan man läsa:
"Värdet fctk/ksi som gräns för uppsprickning bör väljas generellt när det gäller att med viss säkerhetsmarginal undvika sprickor men om det gäller att göra mer sannolika bedömningar av betongens uppsprickning t.ex. vid beräkning av deformationer kan man istället välja fctm eller fctm,fl."
Att det finns två olika kriterier skapar alltså en viss förvirring. Hur bör man tänka i det här fallet?
Svar: Det som står i Betongföreningens handbok är väl klart nog, men det är egentligen bara en kommentar till vad som även kan utläsas ur SS-EN 1992. För att avgöra eventuellt behov av sprickarmering i spännbetong gäller fctk/ksi enligt den svenska tillämpningen av SS-EN 1992, avsnitt 7.3.2 (4) . För beräkning av deformationer använder man däremot normalt fctm eller fctm,fl, vilket framgår av avsnitt 7.4.3 (4).
Fråga: I figur 6.29 i SS-EN 1992-1-1, avsnitt 6.7,är ytan Aco rektangulär, men hur gör man om tryckytan är cirkulär? Ska figuren ses som en illustration för att visa principen för lastspridningen eller måste en cirkulär tryckyta räknas om till en "ekvivalent fyrkant/rektangel"? Kan lastspridningen för en cirkulär tryck yta antas vara en stympad kon med övre och nedre diametern motsvarande b1 respektive b2 i figur 6.29?
Svar: Om tryckytan är cirkulär blir fördelningsytan också cirkulär, det är ju ”den största fördelningsyta likformig med Ac0 över vilken lasten kan fördelas”. Beskrivningen av lastspridningen som en stympad kon etc. är korrekt.
Fråga: Vi undrar över vidhäftningsförmågan i en fog i avsnitt 6.2.5 ekvation (6.25). Vår fråga är om det finns någon teori bakom ekvationen? Har man testat sig fram för att definiera C?
Svar: Det finns en teori bakom ekvationen. Termen c × fctd uttrycker en kombination av vidhäftning p.g.a. kemiska och fysikaliska bindingar, och ojämnheter som hakar i varandra. Vidhäftning förekommer även i en absolut slät och ren fogyta, medan effekten av ojämnheter förutsätter skrovliga ytor, vilket gör att c får högre värden ju skrovligare ytan är.
Termen m*(sc+r*fyd) uttrycker en ren friktion, där m är en friktionskoefficient, som ökar med ökande skrovlighet. Friktion förutsätter tryck vinkelrätt mot ytan, vilket kan åstadkommas av yttre tryck eller armering som korsar fogen; armeringen förutsätts uppnå flytspänning när den sträcks vid glidning i fogen. Om armeringen lutar i förhållandet till fogytan tillkommer en inverkan av armeringskraftens komposant längs fogen.
Så långt teorin som, bortsett från inverkan av armeringens lutning, bara är beskrivande. För att få värden på c och m måste man göra jämförelser med försöksresultat. Värdet på c får man då ur försök där det varken finns yttre tryck eller armering som korsar fogen. Om ni vill fördjupa er i detta kan ni läsa avsnitt 6.3 i "fib Model Code 2010".
Fråga: Finns det något gällande regelverk som styr hur man kan beräkna kapaciteten hos en befintlig betongkonstruktion? Hur kontrollerar man en befintlig konstruktion ifall den håller för en extra belastning som en extra våning utgör?
Svar: Det finns mig veterligt inget regelverk med normstatus för detta än så länge. Det kommer troligen in i Eurokoderna så småningom, men ännu finns inget färdigt.
"fib Model Code for Concrete Structures 2010" säger sig täcka betongkonstruktioners hela livslängd, från projektering och uppförande till bevarande (tillståndsbedömning, underhåll, förstärkning). Det finns ett särskilt kapitel 9 Conservation som behandlar det senare, men det ger mest allmänna principer och inte så mycket konkreta anvisningar.
Kontrollberäkning av befintliga konstruktioner för ökade laster eller andra förändringar är ju ett mycket vanligt problem, som man i stor utsträckning kan hantera med hjälp av dimensioneringsregler för nyprojektering. Skillnaden är huvudsakligen att vid nyprojektering arbetar man med förutsägelser om materialegenskaper, geometri m.m. medan man vid kontrollberäkning av en befintlig konstruktion har möjlighet att mäta verkliga hållfastheter och geometrier, och därmed reducera osäkerheter. Det ger ofta möjlighet till gynnsammare bedömning än om man bara använder värden enligt ritningar, men i praktiken är det mest det senare som tillämpas.
Fråga: Enligt BBK räknade man ut böjningsstyvhet för betong med hjälp av EI=0,8×Ec×Ic/(1+effektivt kryptal) (ekvation (3.4.2.2a)).
Enligt SS-EN 1992 räknar man ut betongsböjningsstyvhet med EI=Kc×Ecd×Ic+Ks×Es×Is (ekvation (5.21)). I den här frågeställningen försummar jag stål-delen av det här uttrycket. Jämför även uttrycket för samverkanspelare i SS-EN 1994, EI(eff)=Ea×Ia+Es×Is+Ke×Ecm×Ic (ekvation (6.40)). Här tas Ke=0,6 enligt normen.
Mitt problem är att när jag jämför de här uttrycken är SS-EN 1992 mycket ogynnsammare än BBK. Kc=k1×k2/(1+effektivt kryptal) (ekvation (5.22) i SS-EN 1992). Om man sätter EI(SS-EN 1992)=EI(BBK) och tar bort (1+effektivt styvhet) från både borde k1×k2 vara ungefär lika med 1. Men k1×k2 blir max 0,26 med C35/45 betong.
Varför blir styvheten så mycket lägre med Eurokoden?
Svar: Uttrycken för nominell styvhet i SS-EN 1992 är framtagna genom kalibrering mot beräkningar enligt generell metod (5.8.6). De uttryck som finns i BBK kan användas på samma sätt, men de är inte lika noggrant kalibrerade, och i samband med kalibreringen av SS-EN 1992:s uttryck visade det sig att BBK:s uttryck i vissa fall kunde vara på osäkra sidan. Detta är förklaringen till att SS-EN 1992 ibland (men inte alltid) ger lägre styvhet än BBK.
Det är viktigt att poängtera att den nominella styvheten är en fiktiv parameter, som inte kan förklaras på annat sätt än att den vid beräkning enligt avsnitt 5.8.7 ska ge en bärförmåga som överensstämmer hyggligt med beräkningar enligt generell metod. Det är således inte en styvhet som ”finns” i verkligheten. Ordet ”hyggligt” syftar på att det i en förhållandevis enkel beräkningsmodell inte är möjligt att erhålla perfekt överensstämmelse med en generell beräkning. Bärförmågan för en slank pelare påverkas av betongens och armeringens icke-linjära arbetskurvor, av uppsprickning, av pelarens utböjning och av krypning på ett mycket komplicerat sätt, vilket endast kan beaktas noggrant med den generella metoden.
Fråga: Hur verifierar man en befintlig betongkonstruktion om den skulle klara av en belastning av sin befintliga last samt även en tilläggsbelastning som skulle bli av en tillbyggnad på höjden?
Svar: Om en konstruktionsdel inte får ökade snittkrafter av en förändring behöver den normalt inte förstärkas, och inte heller kontrolleras enligt aktuellt regelverk.
Om den får ökade snittkrafter bör den kontrolleras enligt aktuella regler. Om den då visar sig ha tillräcklig bärförmåga i befintligt skick behöver den normalt inte heller förstärkas. Problem kan dock uppstå med minimiarmering i balkar, väggar, plattor, väggskivor m.m. Även om konstruktionsdelen skulle ha tillräcklig bärförmåga så har den ofta inte en minimiarmering som motsvarar vad som krävs enligt SS-EN 1992. Ska man då behöva förstärka även med minimiarmering? Det är ju inte så lätt eftersom minimiarmeringen vanligen inte är koncentrerad (undantag: minsta böjarmering för balkar), utan fördelad på olika sätt.
Detta med minimiarmering vid kontrollberäkning av befintliga konstruktioner har varit uppe tidigare och nedan citeras delar av svaret:
”…Eurokoderna gäller i princip för nya konstruktioner, men inte uttryckligen för kontrollberäkning av befintliga konstruktioner. När det gäller broar har ju Trafikverket regler om klassningsberäkningar, men för husbyggnader är det oklart vad som gäller. För närvarande finns bara Eurokoderna att gå efter, och befintliga konstruktioner uppfyller då sällan alla krav på minimiarmering. Det kan nämnas att ett arbete med en ny Eurokod för Kontrollberäkning av befintliga konstruktioner (Assessment of existing structures) har påbörjats, samt att en reviderad EK2 kommer att få ett avsnitt på samma tema. Dessa nya och reviderade Eurokoder kommer dock förmodligen inte ut förrän om flera år.Vi kan inte ge något definitivt svar på hur man ska göra vid ombyggnader, där man är tvungen att kontrollberäkna eller dimensionera för ändrade förutsättningar i något avseende, t.ex. ökad last, håltagning e.d. Där förändringen inte medför ökade snittkrafter eller spänningar bör ju den gamla konstruktionen duga, men vid ökade snittkrafter/spänningar kan ju Eurokodens krav på minimiarmering medföra behov av förstärkning, även om bärförmågan skulle vara tillräcklig med befintlig armering. Det viktigaste är dock att uppfylla krav på bärförmåga. Där armeringen inte når upp till minimikraven måste konstruktören bedöma huruvida armeringen i så fall behöver förstärkas, med hänsyn till vilka konsekvenser eventuella grova sprickor m.m. kan ha på beständighet och andra funktionskrav. En annan viktig sak att beakta är möjligheten till segt brott, vilket är en viktig grund för Eurokodens minimikrav på armering."
I förslag till ändringar i EKS (remisstid till den 1 juni-2015) anges följande:
Avdelning A
2 §
Föreskrifterna gäller även på motsvarande sätt i tillämpliga delar vid uppförande och ändring av andra byggnadsverk än byggnader, där brister i byggnadsverkens bärförmåga, stadga och beständighet kan förorsaka risk för oproportionerligt stora skador.
Krav vid ändring av byggnadsverk
4 § Byggnader ska vid ändring uppfylla de krav på bärförmåga, stadga och beständighet som anges i denna författning för uppförande av nya byggnader.
Som alternativ till eurokoderna får andra verifieringsmodeller användas om dessa ger minst lika eller lägre brottsannolikhet som de som anges i avdelning B, kapitel 0, 1 § för respektive säkerhetsklass.
Allmänt råd
Andra verifieringsmodeller kan vara sådana som tillämpades när byggnaden uppfördes.
Avsteg från säkerhetsnivåerna som anges i avdelning B, kapitel 0, 1 § får göras om det finns särskilda skäl med hänsyn till byggnadens förutsättningar och ändringens omfattning. Regler om detta finns i 7 § i denna avdelning.
Reglerna om material, projektering, utförande, dimensionering och kontroll i denna avdelning gäller i tillämpliga delar vid ändring av byggnader."
Fråga: Jag har en fråga angående tvärkraftsöverföring i fogar SS-EN 1992-1-1:2005, avsnitt 6.2.5 och ekvation (6.25). Då betongarean är betydligt större än stålarean som korsar fogen i normala fogar mellan prefabricerade element, bidrar stålet marginalt till tvärkraftskapaciteten i fogen. Jämförs beräkningen med tvärkraftskapacitet av dymling enligt BBK04 avsnitt 6.8.3, bidrar stålmängden mycket mer. Finns det någon motsvarhet till beräkning av dymling i SS-EN 1992 eller är det ekvation (6.25) i SS-EN 1992 som skall följas?
Kan ni i så fall förklara hur tvärkapaciteten för en dragen slät fog (b=150mm) där yttre kraft sätts till 0 med Ø20s1m endast blir 0.2 kN/m. ρ= 0.0021. Borde det inte istället vara utragningsbrott av armeringsjärnen som ger kapaciteten. Varför sätts inte ρ = 1.0 då betongens kapacitet är = 0?
Svar: Bärförmågan för en dymling enligt BBK är normalt mycket lägre än den som erhålls med SS-EN 1992 ekvation (6.25), och även i jämförelse med BBK:s motsvarighet ekvation (3.11.3). Dessa ekvationer uttrycker bärförmågan som en skjuvspänning, kraft per ytenhet, som hänför sig till fogens area, inte stålets (vilket frågeställaren tycks utgå från). Den term som är beroende av armeringsinnehållet uttrycker en friktion, där skjuvkraften är lika med flytkraften i armeringen gånger en friktionskoefficient m.
Dragen slät fog (c=0,m=0,5) ger en bärförmåga, här uttryckt som kraft/längdenhet i ställer för kraft per ytenhet:
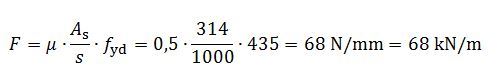
SS-EN 1992 ger inget uttryck för dymlingkraft, men inget hindrar att man använder BBK:s uttryck. Detta bygger på en enkel mekanisk modell som är lätt att härleda. Man måste bara se upp så att dymlingskraften inte är excentrisk i förhållande till betongytan samt att det inte samtidigt förekommer dragkraft i dymlingen, i vilka fall bärförmågan blir lägre. Detta påpekas inte särskilt i BBK, men framgår underförstått av figurer. Inverkan av excentricitet och/eller dragkraft kan dock lätt härledas med hjälp av modellen, som bygger på att flytmoment uppnås i stången samtidigt som betongen tar ”präglingstryck” 3fcd.
I exemplet skulle dymlingsverkan ge, om betongen är C30:
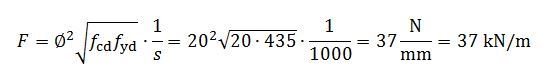
Fråga: Var i Eurokoden kan man hitta dimensioneringsregler för gjutning av vattentäta konstruktioner under grundvattenyta?
Svar: SS-EN 1992-3 a 7, behandlar vattentäthet i behållare och liknande konstruktioner. Detta bör kunna tillämpas även för grundkonstruktioner under grundvattenytan som ska vara täta.
Fråga: När man beräknar sprickor i betongkonstruktioner behöver man i BBK inte sätta medelsprickavståndet Srm större än tvärstängers inbördes avstånd (t.ex. armeringsnät). Finns det någon sådan regel i SS-EN 1992 också?
Svar: Nej, någon motsvarande regel finns inte i SS-EN 1992.
Fråga: Vilka regler finns för grundläggning med betongplintar på berg när det gäller restriktioner och specifika krav?
Svar: De enda regler som berör grundplintar på berg finns i avsnitt 9.8.4.
Den nationellt valbara parametern q2, med rekommenderat värde 5 MPa, har av Trafikverket satts till 1 MPa. Att ge ett fixt värde i MPa är dock ologiskt, då risken för spjälkning inte bara beror av grundtrycket utan även av geometrin. Om tryckkraften är jämnt fördelad över hela plintens area så blir det ju ingen spjälkning, oavsett grundtryck. I Boverkets EKS sägs därför istället att q2 är ”det grundtryck som vid aktuell geometri orsakar spjälkning i betongen”.
Tyvärr ger varken SS-EN 1992 eller EKS någon anvisning om hur man ska avgöra när spjälkning kan inträffa. Den formel för spjälkkraften som ges är i princip identisk med den som ges för partiell diskontinuitet i 6.5.3, fast med andra beteckningar. Den andra regeln är minsta diameter för armering i plintar på berg, där rekommenderat värde väljs i EKS.
Fråga: Några frågor kring avståndsbegränsning och armeringsmängd i kapitel 9.
Enligt avsnitt 9.6.2 (3) skall avståndet mellan vertikala stänger begränsas till det mindre av tre gånger väggtjockleken och 400mm. Gäller detta hela armeringsmängden, eller räcker det att delar av armeringen uppfyller kraven? Ett exempel kan tas från Prefabindustrin, där nät 5150 (131mm2/m) ofta används som grundarmering. Vid en vägg med 200 mm tjocklek kan minimikravet enligt avsnitt 9.6.2 (1) beräknas som 0,002 Ac = 0,002 × 200 × 1000=400 mm2/m, eller ”200 mm2/m och sida” (enligt 9.6.2 (2) skall den fördelas jämt på väggytorna). För att uppnå den mängden kan stänger med Ø 8 läggas in med cc 450 (112 mm2/m) vilket ger en tillräcklig mängd (243 mm2/m per sida) samt enkelt utförande då en Ø8 kan najas fast vid var tredje stång i nätet. Armeringstängernas delning uppfyller dock inte kravet med max avstånd på min{3 gånger väggtjockleken; 400}. Kan denna lösning godtas då mer än hälften av armeringsmängden ligger tätare? Då nätet är svetsat borde de liggande stängerna kunna bidra till god lastspridning till.
Samma princip gäller 9.6.3 (2); skall all horisontell armering ha angiven maximalt inbördes avstånd?
Avsnitt 9.6.3 (1) anger att horisontell minimiarmering är max{25 % av stående armering; 0,001 Ac}. Innebär detta att man ska lägga in 25 % av vertikal minimiarmering för det stället, eller 25 % av den vertikala armering som krävs statiskt? Om man exempelvis har en vägg som på en sträcka klarar sig med vertikal minimiarmering = 0,002 Ac enligt avsnitt 9.6.2 och på en sträcka behöver det dubbla för att lasten är högre, kan man då ha lika horisontell armering längs hela väggen eller måste den också öka när den vertikala armeringsmängden ökar?
Svar: Första frågan: Den armering som uppfyller avståndskriteriet (5 s 150) uppfyller inte areakriteriet enligt (1), och den armering som uppfyller areakriteriet (8 s 450) uppfyller inte avståndskriteriet enligt (3). Jag tycker ändå att man bör acceptera den totala armering som beskrivs i exemplet. Avståndet mellan vertikala stänger är ju de facto mindre än 400 mm, och det står egentligen inte i (3) att avståndet nödvändigtvis gäller stänger med samma diameter.
Andra frågan: Samma tolkning som ovan kan göras. I det aktuella fallet finns horisontella stänger på mindre avstånd än 400 mm.
Tredje frågan: Horisontell armering bör relateras till aktuell vertikal armering, oavsett om denna är minimiarmering eller statiskt bestämd. Om man lägger in olika vertikal armering i olika delar av en vägg beroende på statiskt behov, så bör den horisontella armeringen anpassas därefter, d.v.s. antingen bör all horisontell armering vara minst 25 % av den största vertikala armeringen, eller så varierar man den horisontella armeringen efter den vertikala armeringens variation.
Det är bra att ingenjörer tänker själv. Boverket har inga synpunkter varken på frågeställarens lösning eller på expertens svar för fråga 1 och fråga 2. Det gäller att ha i åtanke att regler finns för att konstruktioner inte ska kollapsa och äventyra människors hälsa och säkerhet.
När det gäller krav på minsta mängd horisontell armering i en vägg får man även här ha i åtanke vad syftet med regeln är. Här handlar det om så kallad ”robusthet”. Det finns inget skäl att anta att robustheten skulle äventyras av att mängden horisontell armeringen utgår från den mängd vertikal armering som krävs med avseende på bärförmågan.
För övrigt ändrar Boverket krav på minimiarmering i kommande EKS 10. I den ställs inga krav på minimiarmering i väggar om väggen inte är alltför slank. Det är den statiska beräkningen som ligger till grund för mängden armering. Om väggen inte behöver armering, men är alltför slank gäller enligt ändringen As,vmin = 0,001 Ac.
EKS 10 träder ikraft den 1 januari 2016 om inget oförutsett inträffar.
Fråga: Dimensionerar en platta på mark som är byggd på så sätt att den kan krympa fritt åt alla håll. Plattan ska dock vara vattentät och jag tänkte då sprickarmera plattan. I Betongrapport 15, s 97, gör man en tolkning på beräkning av sprickbredd på grund av förhindrad krympning. Men tittar där på töjningsskillnaden mellan betong och armering. Hur ser ni på det? Är detta en möjlig väg att gå om man vill ta fram sprickarmering för en platta som tillåts krympa fritt?
Svar: Om plattan är byggd så att den verkligen kan krympa fritt så uppstår ju inga krympsprickor, och då behövs i princip ingen sprickarmering med hänsyn till förhindrad krympning. Om man ändå vill räkna med att krympsprickor kan uppstå så är metoden i Betongrapport 15 en möjlig väg att begränsa sprickbredden. Sprickarmeringen måste dock minst uppfylla kravet på minimiarmering enligt SS-EN 1992 avsnitt 7.3.2, med 
Krympsprickor uppstår då den fria krympningen förhindras av olika låsningar, t.ex. friktionen mot underlaget (marken) under plattan i detta fall, vilket ger tvångsspänningar. Ett alternativt sätt att beräkna sprickbredden på sprickor uppkomna av tvång, särskilt om krav ställs på konstruktionsdelens vattentäthet, är att använda anvisningarna i SS-EN 1992-3 bilagor L och M.
Fråga: Vi undersöker vad som finns skrivet i SS-EN 1992-1-1 om dimensionering av väggar och har då en fundering över ekvation 12.10 som innehåller en faktor enligt ekvation 12.11. Är det möjligt att hitta några bakgrundsfakta om hur den faktorn är framtagen?
Svar: Ekvation 12.11 är felaktig och beaktar inte krypning. Den ger därför resultat på osäkra sidan för normala fall, där krypning kan ha stor inverkan. En rättelse har införts, men den är inte till någon hjälp, då den visserligen ger en faktor som ska beakta krypning, men det ges inget uttryck för denna faktor.
I nedanstående artikel ges ett förslag till slutet uttryck för bärförmågan hos oarmerade väggar, som beaktar krypning och ger god överensstämmelse med noggranna beräkningar, generell metod enligt SS-EN2 5.8.6. Förslaget blev inte antaget, men det bör kunna användas i brist på lämpligt uttryck i EK2.
Westerberg B: Load bearing capacity of unreinforced walls. Design of concrete structures and bridges using Eurocodes, Bratislava 12-13 September 2011.
Fråga: Jag har en fråga ang. ramhörnsarmering enligt SS-EN 1992-1-1, Bilaga J-2-3. Finns några geometriska krav (jmf Bro 2004, 42.641)
Svar: Det finns inga andra regler än de som ges i J.2.3. Någon motsvarighet till det geometriska kriteriet beträffande framtass för stödmur i som anges Bro 2004 42.641 finns således inte. Om det är detta som frågan åsyftar, så finns inget som hindrar att man tillämpar det även vid användning av Eurokoden, eftersom det inte står något i Eurokoden som det kan motsäga.
Fråga: Har en fråga angående ekvation (7.18) och kontroll av deformationer genom beräkning med SS-EN 1992-1-1. Ska det vara alfa eller ska vara delta?
Svar: Det spelar ingen roll vilken bokstav man använder; a kan stå för antingen krökning, vinkeländring eller nedböjning, precis som det står i texten.
Om man låter a beteckna krökning så används formeln för beräkning av krökning i ett tillräckligt stort antal tvärsnitt, för att man sedan ska kunna integrera sig fram till vinkeländring och/eller nedböjning. Detta är det noggrannaste sättet att beräkna deformationer, och det som ger störst nytta av dragen betong mellan sprickor (vilket är det som beaktas med parametern z ), då man i så fall beräknar z separat för varje tvärsnitt.
Som förenkling kan man låta a beteckna t.ex. maximal vinkeländring eller maximal nedböjning. I så fall blir inverkan av dragen betong mellan sprickor mindre, eftersom man då bör basera z på tvärsnitt med största moment, vilket ger resultat mer eller mindre på säkra sidan.
Fråga: Min fråga rör sprickvidd i armerad betong. För de flesta fall beräknas sprickavståndet Sr,max enligt ekvation (7.11) under avsnitt 7.3.4. Uttrycket kan generera avstånd över 1 m med stora sprickvidder som följd för små armeringsmängder. Om armeringsmängden minskas eller armering utesluts är ekvation (7.14) i samma avsnitt tillämpbart. Detta uttryck ger ofta betydligt tätare sprickavstånd, alltså trots minskning av armeringsmängden.
Kan ekvation (7.14) ses som övre begränsning av ekvation (7.11), alltså Sr,max = min (7.11, 7.14)? Om inte, varför blir det drastiska förbättringen av sprickdelning om armeringsmängden minskas?
Svar: Ekvation (7.14) ger en övre gräns för den beräknade sprickbredden, som det står i texten. Om man minskar armeringsmängden så att sprickavståndet enligt (7.11) blir större än enligt (7.14), så kan man alltså använda det senare.
Ekvation (7.11) gäller för centrumavstånd s ≤ 5(c + ø/2) och gäller som (7.14) ”övre gräns” om s > 5(c + ø/2). I de flesta fall ger (7.14) större sprickavstånd än (7.11) så länge s ≤ 5(c + ø/2), och då finns ju inget att vinna med att räkna med mindre armering så att (7.14) blir tillämplig.
I vissa fall, närmare bestämt vid stor stångdiameter i förhållande till effektiva höjden, kan ekvation (7.14) ge mindre sprickavstånd än (7.11) även om s ≤ 5(c + ø/2), och i sådana fall kan det ”löna sig” att minska armeringen så att (7.14) blir tillämplig (d.v.s. så att s > 5(c + ø/2)). De fall där detta kan inträffa har dock mycket stor stångdiameter i förhållande till effektiva höjden, och torde vara sällsynta.
Figuren nedan illustrerar ett sådant fall schematiskt, och det föreslås att man följer den röda heldragna linjen, istället för den blå streckade. Det upprepas att sådana här fall är sällsynta, och att ekvation (7.11) i de flesta fall ger mindre beräknad sprickbredd än ekvation (7.14) för s ≤ 5(c + ø/2).
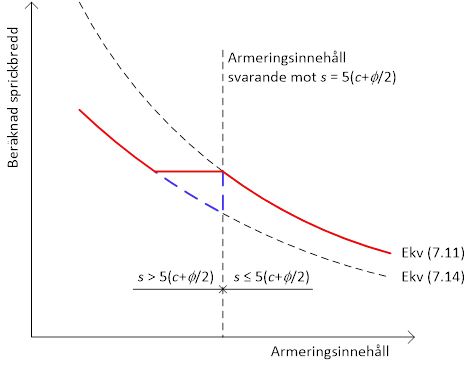
Avslutningsvis rekommenderas, att om det finns krav på sprickbreddsbegränsning, så bör armeringens centrumavstånd inte överstiga 5(c + ø/2). I så fall är det alltid ekvation (7.11) som gäller, och då uppstår aldrig den fråga som här behandlats.
Fråga: Jag undrar över avsnitt 9.3.1.1 Massiva plattor och den minimiarmeringen i tvärled som står som 20 % av huvudarmeringen. Där står det att det gäller för enkelspända plattor. Står det något om minsta tillåtna tvärledsarmering för 3- eller 4-sidigt upplagda plattor?
Var i Eurokoderna att man inte får räkna med skarven som kraftöverförande-/momentöverförande? Det låter lite konstigt om man inte skulle få räkna den som det och då skulle ju man bli tvungen att räkna alla plattbärlag som enkelspända.
Svar: För 3- eller 4-sidigt upplagda plattor dimensioneras armeringen av moment i båda riktningarna, och då gäller 9.3.1.1 (1), med hänvisning till 9.2.1.1 (1), för vardera riktningen. Enkelspända plattor kan sakna dimensionerande moment i sekundärriktningen, och då gäller 9.3.1.1 (2).
Det finns ingen speciell regel om plattbärlag i SS-EN 1992. Huruvida en skarv kan räknas som kraft/momentöverförande beror på platsbetongens armering och tjocklek m.m., själva plattbärlaget kan ju normalt inte ta något.
Fråga: Vart finns information om att man ta fram ”eccentricity due to creep” som tillkommer med SS-EN 1992-1-1:2005/A1:2014, se urklipp nedanför?
Svar: Tyvärr hittar man inte denna faktor någonstans. Tidigare sades att formeln beaktade ”normala effekter av krypning”, men det gjorde den inte alls, med påföljd att resultatet i normala fall blev på osäkra sidan. Detta är bakgrunden till ändringen, som framhäver inverkan av krypning, men det blev tyvärr bara en halvmesyr, eftersom man inte ger någon konkret anvisning om hur inverkan av krypning ska beaktas.
Det finns ett förslag till formel, som beaktar alla effekter på ett rimligt sätt, inklusive krypning, men det har inte blivit antaget. Förslaget bygger på jämförelse med resultat enligt noggrann icke-linjär analys (generell metod enligt 5.8.6), och ger mycket god överensstämmelse med en sådan.
Det beskrivs i följande artikel:
Westerberg, B: Load bearing capacity of unreinforced concrete walls. Conference Design of concrete structures and bridges. Slovak University of Technology, Bratislava, 12-13 September 2011.
Artikeln kan laddas ner här.
Publicerad 2016-09-26
Fråga: Har en fråga angående m-faktorn som gäller vid snedställningslast för hela det stabiliserande systemet i betonghus (SS-EN 1992-1-1 kap 5.2):
När det gäller snedställningslast för ett stabiliserande system så måste man ange antal vertikala delar (m-faktorn). I betongrapport nr 15 presenteras ett exempel där man använder de antal vertikala delar totalt i huset och delar på 2 eftersom de har två stabiliserande trapphus. Detta blir m-faktorn.
Om man inte har så ”snäll” geometri utan t.ex. enbart har stabiliserande enheter i 3 av husets 4 ytterväggar med en styv skiva där då t.ex. en vägg upptar all stabiliserande yttrekraft och de andra balanserar momentet som uppstår i konstruktionen, hur ska man tänka då med m-antalet?
Om de stabiliserande enheterna inte är så symmetriskt placerade och/eller kanske har olika styvheter, hur resonerar man då?
Följdfråga: Jag är nöjd med svaret på första frågan (m-antal vid stabiliserande enheter i 3 väggar) men skulle vilja ha lite vägledning i följdfrågan jag ställer i det sista stycket i mitt frågemail. Jag bifogar en förklarande skiss. Hur resonerar man här för valet av antalet m?
Svar: Grundprincipen är att m är antalet vertikallastbärande enheter, vars snedställning skulle kunna bidra till horisontallasten på den aktuella stabiliserande enheten. Inverkan av m är statistisk, d.v.s. ju fler enheter som ingår desto mindre är sannolikheten för att de ska luta åt samma håll. Som en enhet kan man betrakta t.ex. en pelare eller ett väggelement i en våning (de kan luta olika i olika våningar).
Ett exempel med osymmetriskt stabiliserande system skulle kunna se ut så här:
Antalet m kan i detta fall sättas till antalet pelare plus antalet väggelement (om väggen består av element), gånger ett visst antal våningar:
Följdfråga: Det här med antalet m är ingen exakt vetenskap, här kan finnas utrymme för egna bedömningar. Nedanstående är ett förslag till tolkning för de givna exemplen.
Alla tre exemplen har ett statiskt bestämt stabiliserande system. Det betyder att det inte spelar någon roll om de båda tornen har lika eller olika styvhet. Fördelningen av kraft på tornen bestäms istället helt av geometrin. I den meningen skiljer sig inte fall 3 från de övriga.
Om geometrin ger lika kraft på båda tornen (fall 1 och 3) kan man lämpligen för vart och ett av dem sätta m till hälften av det totala antalet element. Tanken är att krafterna på det vänstra tornet i påverkas obetydligt av snedställning i den högra halvan av huset, och tvärtom.
Om geometrin ger olika kraft på respektive torn (fall 2) kan man istället dela upp det totala antalet så att vartdera tornet får en andel proportionell mot dess andel av den totala kraften.
Med ”total kraft” menas här den totala inverkan av vindlast. Eftersom det i fall 2 skulle kunna bli olika bidrag från snedställning på vartdera tornet (även om den inverkan mestadels blir liten) så behöver man kanske inte krångla till det genom att även inkludera snedställningskraften i den ”totala kraften”. Vill man det så är det naturligtvis inte ”förbjudet”, men det kan kanske ge behov av iteration.
Publicerad 2016-09-26
Fråga: Under avsnitt 8.7.2 (3) står det "det fria avståndet mellan stänger som omlottskarvas bör inte överstiga 4Ø eller 50 mm. I annat fall bör skarvlängden ökas med en sträcka motsvarande det fria avståndets överskridande av 4Ø eller 50mm. Menas detta procentuellt? Eller kan man t.ex. öka det fria avståndet med 30mm om man ökar skarvlängden med 30 mm?
Svar: Ökningen avser absolut mått. Man kan alltså t.ex. öka avståndet med 30 mm om man ökar skarvlängden med 30 mm.
Publicerad 2016-09-26
Fråga: Jag har en fråga angående frånvaro av dragspänningar, se avsnitt 7.3.1 (105). Tidigare stod det i Bro 2004 (42.312) att 100 mm var från centrum spännenhet/foderrör. Kan jag göra samma tolkning i det här fallet, d.v.s. cc-mått? Texten i SS-EN 1992-2 är skriven som att avståndet skulle kunna vara kant-kant spännenheter.
Svar: Eftersom det inte anges någon närmare precisering kan man anta att kravet gäller från närmaste kant på spännarmering eller ursparingsrör till den punkt där spänningen är noll.
Publicerad 2016-09-26
Fråga: I bilaga NN ges två tabeller. NN.1 och NN.2.
När utmattning i tvärled för en brobaneplatta (vägbro) ska kontrollera ska man då använda armeringstypen c) i tabell NN.2 för både stödområde och fältområde?
Min tanke var att beakta fältområde enligt tabell NN.1 och stödområde enligt NN.2 som kontinuerlig balk (a)).
Svar: Orden ”lokalt” och ”brobaneplatta” i tabell NN.2 är tillämpliga på alla delar av en brobaneplatta.
Publicerad 2016-09-26
Fråga: Jag har lite problem med att förstå klausul (113) i SS-EN 1992-3:2006. Undrar dessutom vad det är för enhet på värdet 15010–6?
Svar: För den händelse du inte har tillgång till den svenska översättningen så lyder den:
”Om villkoren i 7.3.1 (111) för täthetsklass 1 uppfylls kan vattenförande sprickor förväntas självläka, såvida det inte förekommer väsentliga variationer i last eller temperatur under drift. I avsaknad av mer tillförlitlig information kan självläkning förutsättas om töjningsvidden under drift understiger 15010–6.”
Innebörden är att genomgående sprickor som inte överstiger 0,2 mm kan förväntas självläka, förutsatt att töjningsvariationer, t.ex. p.g.a. last eller temperaturvariationer, inte är större än 15010–6(dimensionslös). Töjningsvidd avser töjning i armering.
En töjningsvidd på 15010–6 kan också skrivas som De = 0,15 ‰.
Denna töjningsvidd avser dock variationer av töjningen i armeringen beräknad i stadium II, d.v.s. i sprucket stadium.
Publicerad 2016-09-26
Fråga: Det råder en viss förvirring bland våra kunder när det gäller de i många fall mycket varierande resultat som erhålls när det gäller knäckkapacitet för de tre metoderna styvhetsmetoden, krökningsmetoden och den generella metoden. Speciellt för väggar blir ofta kapaciteten för styvhetsmetoden orealistiskt låg.
Ett exempel: Vägg med höjd 4 m och tjocklek 0.15 m. Betong C30/37, armering 6+6 Ø 6 B500. Täckskikt 20 mm. Effektivt kryptal 2.0. Initialkrokighet l/400. Beräkna kapacitet för centrisk vertikal last. Styvhetsmetoden ger ca 154 kN (verifierat med program och handberäkning), Krökningsmetoden 620 kN, (verifierat med program och handberäkning), den generella metoden 766 kN verifierat med program. Vid jämförelse med diagram framtagna av Bo Westerberg för den generella metoden ger oarmerad vägg ca 800 kN med de aktuella förutsättningarna. Om man utökar jämförelsen till den tidigare metoden enligt BBK 04 avsnitt 6.3.3.2 och väljer säkerhetsklass 1 eftersom säkerheten numera ligger på lastsidan erhålls kapaciteten ca 980 kN.
När det gäller styvhetsmetoden och BBK:s metod kan knäcklasten enkelt delas upp i en betongdel och en armeringsdel. Man finner då att för styvhetsmetoden gäller Nk_betong = 54 kN och Nk_armering = 113 kN. För BBK:s metod gäller Nk_betong = 945 kN och Nk_armering 39 kN. Ganska avsevärd skillnad och har kontrollerat beräkningarna noga så jag tror detta stämmer.
Sammanfattning: Det verkar alltså i många fall, speciellt för väggar, som om variationen blir alldeles orealistiskt stor och resultaten för styvhetsmetoden blir minst sagt underliga. Vore intressant att få frågan belyst.
Svar: Styvhetsmetoden och krökningsmetoden i SS-EN 1992 är båda starkt förenklade metoder, som har kalibrerats mot resultat enligt generell metod. Båda metoderna är en kompromiss mellan enkelhet och noggrannhet. Det går inte att få god överensstämmelse med generell metod med i hela registret någorlunda enkelhet. Av de båda metoderna kan ibland den ena, ibland den andra ge gynnsammare resultat. I Sverige är båda metoderna tillåtna. Krökningsmetoden fanns även i ENV-versionen av SS-EN 1992, men har kompletterats med en faktor som beaktar krypning. Styvhetsmetoden har en enklare motsvarighet i BBK.
Uppdelning på en ”betongterm” och en ”armeringsterm” i styvhetsmetoden är helt fiktiv, och säger egentligen ingenting. Kalibreringen av ”betongtermen” är baserad på Ks = 1. Man hade även kunnat utgå från ett annat värde på Ks, t.ex. 0,5 eller ett värde som beror av olika parametrar, men då hade storleksförhållandet mellan de båda termerna hade blivit en annan.
Vid jämförelse med BBK uppdagades att BBK i vissa fall kunde ge resultat på osäkra sidan i förhållande till generell metod, vilket förklarar varför man kan hitta exempel där SS-EN 1992 ger lägre bärförmåga än BBK.
Publicerad 2016-10-24
Fråga: Jag skulle behöva ha hjälp att tolka figur 9.10b i avsnitt 9.4.3. Ska j-bygelns nedre bock närmast pelare placeras 2d från pelare eller inom 2d från pelaren? Jag tolkar figuren, med texten ≅2d som att den ska vara 2d ifrån, men jag tror inte det ska vara så?
Svar: Figuren bör tolkas så att den innersta bygelns nedre bock bör ligga ca 2d från pelaren.
Publicerad 2016-10-24
Fråga: I SS-EN 1992-1-1 men även i de nationella tillämpningsstandarderna så begränsar man sig till en karakteristisk sprickbredd. Vad är definitionen? Mäts denna på armeringsnivå eller ytnivån?
Svar: Den beräknade sprickbredden bör närmast antas avse nivån för armeringens tyngdpunkt.
Det spelar dock egentligen ingen roll om beräkningen avser sprickbredd vid armeringen eller vid ytan. Den beräknade sprickbredden är endast avsedd att jämföras med ett krav, som avser beräknad sprickbredd, inte med verklig sprickbredd. När man jämför beräknade och verkliga sprickbredder stämmer det sällan, dels beroende på att sprickbredden är ett fenomen med mycket stor spridning, dels beroende på systematiska avvikelser mellan beräkningsförutsättningar och förutsättningar i en verklig konstruktion.
Beräkningar utgår från ”pessimistiska” förutsättningar ifråga om laster, materialegenskaper och armeringens vidhäftningsegenskaper. Den långtidslast man räknar med föreligger kanske inte vid mättillfället, och har ofta ännu aldrig uppnåtts. Den verkliga draghållfastheten i betongen är förmodligen mycket högre än den karakteristiska hållfasthet man räknar med. Armeringen har ofta betydligt bättre vidhäftningsegenskaper än de minimivärden som ligger till grund för sprickbreddsberäkningen. Uppmätta sprickbredder kan därför vara betydligt mindre än beräknade, men man ska då komma ihåg att kraven gäller beräknade värden. Sprickbreddskrav och metoder för att beräkna sprickbredder syftar till att styra armeringsutformningen i en lämplig riktning. Att ställa krav på verkliga sprickbredder är knappast meningsfullt, eftersom det inte finns något att mäta vid projekteringen.
Publicerad 2016-10-24
Fråga: I nya EKS 10 avsnitt 9.2(1) gäller för betongväggar att Asv_min= 0 om lc/b < 18. Vi har i anslutning till detta följande frågor:
Fall 1. lc/b > 18
Vertikal Armering
Asvmin = Max (0.001Ac, cc=400mm, cc=3h)
Horisontell armering
Enligt 9.6.3 (1) gäller enligt EKS 10 Ash_min = (0.25 Asv, cc=400)
Fall2 lc/b < 18
Vertikal Armering
Fråga 1:
I det här fallet är Asvmin=0. Gäller det bara kravet enligt avsnitt 9.6.2 (1) eller även 9.6.2 (3)?
Fråga 2:
Gäller Asvmin=0 så fort lc/b < 18 eller måste man kontrollera om betongens kapacitet överskrids d.v.s. så fort någon armering behövs överhuvudtaget så gäller istället Asvmin = Max (0.001Ac, cc=400mm, cc=3h) liksom för fallet lc/b > 18?
Horisontell armering
Fråga 3:
Gäller förhållandet lc/b endast vertikal armering eller även horisontell?
Om inte borde även här gälla Ashmin = (0.25 Asv, cc=400)
Kommentar: Om Asvmin=0 kan man enligt ovan få minimiarmering horisontellt men ingen vertikalt vilket känns ologiskt.
Svar: Den nya regeln till 9.6.2 (1) i EKS 10 kan möjligen missförstås som att oarmerade väggar endast skulle vara tillåtna för h/b 18. Kapitel 12 gäller dock, och enligt 12.1 (2) kan väggar göras oarmerade oavsett slankhet, utan möjlighet till nationell avvikelse.
Regeln om minimiarmering i 9.6.2 (1) och i EKS 10 definierar vad som kan betraktas, och dimensioneras, som en armerad vägg. För h/b > 18 ska den vertikala armeringen då vara minst As,vmin = 0,001Ac. För h/b 18 kan en vägg enligt EKS 10 betraktas som armerad även med mindre vertikal armering, utan undre gräns, d.v.s. endast dimensioneringen styr.
Den horisontella armeringen bör vara minst 25 % av den aktuella vertikala armeringen; om denna är mindre än 0,001Ac blir alltså den horisontella armeringen motsvarande mindre.
9.6.2 (3) bör tillämpas även om Asv < 0,001Ac.
Svaren på frågorna blir således:
1. Om Asvmin = 0 så är även Ashmin = 0.
2. Om lc/b < 18 så bestäms eventuell armering enbart m.h.t. bärförmåga.
3. För lc/b < 18 är Ashmin = 0, annars 0,25 × Asvmin.
Beträffande oarmerade väggar kan tilläggas att man i en rättelselista nu har lagt till en excentricit i ekvation (12.12) som ska beakta krypning, dock utan någon anvisning om hur denna kan beräknas.
Publicerad 2016-10-24
Fråga: När man ska räkna ut kryptalet är en av faktorerna den ekvivalenta tjockleken (h0)och en av parametrarna för att räkna ut denna är tvärsnittsarean (Ac). Om jag räknar på t.ex. en platta eller en vägg, använder jag då tjockleken som tvärsnittsarea, d.v.s. att man räknar på en meters bredd?
Svar: Den ekvivalenta tjockleken avses svara mot tjockleken för en platta (eller vägg) med samma uttorkningshastighet som det aktuella tvärsnittet. För en platta (eller vägg) med stor utsträckning i förhållande till tjockleken (eller förhindrad uttorkning längs kanterna) är således den ekvivalenta tjockleken lika med tjockleken.
Detta förutsätter att plattan kan torka ut på båda sidorna. För en platta som bara kan torka ut åt ena hållet (t.ex. en platta på mark) blir den ekvivalenta tjockleken lika med dubbla plattjockleken.
Man behöver egentligen bara tänka på att u i uttrycket 2A/u är den sammanlagda längden för de sidor där uttorkning sker.
Publicerad 2016-10-24
Fråga:
Fråga 1:
Enligt 6.1 (109) metod a) ska spänningsarean reduceras så att den tillsammans med moment enligt frekvent lastkombination ger en maximal dragspänning lika med fctm. Momentkapaciteten ska sedan beräknas med denna reducerade spänningsarea. I några snitt i en kontinuerlig balk har jag reducerat bort alla kablar utan att dragspänningen fctm uppnås. Hur hanteras detta fall? Anses det ospruckna tvärsnittet klara bärförmågan enligt metod a) ? Då spänningsarean är 0 blir momentkapaciteten 0 i dessa snitt.
Fråga 2:
Är det endast hela kablar som spänningsarean ska reducera med eller kan andelar av kablar frånräknas?
Svar:
Fråga 1:
Även om den efterspända armeringens spänningsarea är nedräknad till 0 så återstår kan den ospända armeringen i tvärsnittet räknas med vid bestämningen av momentkapacitet. Momentet borde därmed bli > 0.
Fråga 2:
Beräkningen baseras på area. Arean behöver inte delas upp i kablar.
Publicerad 2016-10-24
Fråga: Enligt SS-EN 1992–2 Kap 7, så gäller inte 7.3.3(5) i SS-EN 1992-1-1.
När det gäller beräkning av skjuvsprickor i balkliv så finns en beräkningsmodell beskriven i Betongrapport nr 15, kap. X6. Men hur hanteras lämpligen begränsning av sprickor för längsgående spänningar av vridning i kombination med böjande moment?
Svar: Den metod som beskrivs i avsnitt X6 i handboken bygger på att man beräknar de armeringsspänningar som skulle ge jämvikt med spänningar beräknade för osprucken betong, såsom illustreras i figur X6-1 b). Inverkan av böjande moment ingår då i spänningen sx medan txy härrör från tvärkraft och vridande moment; sy är vanligen liten. I övrigt hänvisas till handboken.
Publicerad 2017-05-30
Fråga: I kapitel "5.8.5 Analysmetoder" får man välja mellan metod på nominell styvhet och nominell krökning för att analysera andra ordningens effekter på enskilda delar.
I kapitel "5.8.7.2 Nominell styvhet" ger ekvation (5.21) ett uttryck för att uppskatta den nominella styvheten EI hos en bärverksdel, denna styvheten kan sedan användas för att kontrollera max knäcklast för bärverket enligt Eulers knäckningsformel tillsammans med dimensionerande moment enl. ekvation (5.28) för att verifiera bärverkets bärförmåga.
Om man istället väljer metoden baserad på nominell krökning i kap 5.8.8 och kontrollerar bärverkets momentkapacitet mot ekvation (5.31) ska man då fortfarande använda EI ur ekvation 5.21 (som ligger under kapitlet nominell styvhet) för att kontrollera max knäcklast enligt Eulers knäckningsformel för bärverksdelen?
Svar: Om man väljer metoden med nominell krökning kommer styvhet och knäckningslast överhuvudtaget aldrig in i bilden. Ekv (5.31) ger ett ”komplett” andra ordningens moment som adderas till första ordningens, och därmed är all andra ordningens inverkan beaktad.
Styvhetsmetoden går inte ut på att kontrollera ”max knäcklast enligt Euler”. Knäckningslasten är ointressant i sig, annat än som en beräkningsparameter som kan användas för beräkning av andra ordningens moment. Ekv (5.28) och (5.30) är exempel på hur en nominell knäckningslast kan användas som beräkningsparameter, men det går att göra en linjär andra ordningens analys med nominell styvhet även utan knäckningslast.
Slutligen påpekas att den knäckningslast som omtalas här är en nominell sådan. Den har ingenting att göra med någon ”verklig” knäcklast, eftersom den ska grundas på en nominell styvhet som innefattar inverkan av icke linjära arbetskurvor, eventuell uppsprickning samt krypning, i ett brottgränstillstånd som även innefattar moment, excentriciteter och deformationer. Uttryck för den nominella styvheten är framtagna genom kalibrering mot generell metod enligt 5.8.6 (icke linjär andra ordningens analys).
Publicerad 2017-05-30
Fråga: I stycke 8.7.2 Omlottskarvar, i punkt (3) så finns det rekommendationer för placering av stänger man bör följa, sedan i punkt (4) så tillåter man att i ett snitt skarva 100 % av stängerna i ett lager om utformningen stämmer överens med punkt (3).
Jag tolkar punkt (4) som att för att man skall få skarva 100 % i ett snitt/lager så måste alla placeringsvillkoren enl. punkt (3) uppfyllas.
Denna tolkning innebär att i en koncentrerad skarv (t.ex. inspänning av prefabricerad balkong i bjälklag) så ska utsticken på vartannat järn vara från L0 till >2,3 × L0, och i och med denna placeringen hamnar ingen skarv i samma snitt utifrån skarvcentra (± 0,65 × L0) vilket inte ger någon förstoring på L0 genom α6=1,0 då andelen skarvar är <25 %. (Längd utstickande järn = >2,3 × Lb,rqd)
Är denna tolkning korrekt eller får man frångå placeringen av stänger enl. punkt (3) och ändå skarva 100 % i ett snitt/lager och då istället använda α6=1,5 för att förstora L0 då andelen skarvar >50 %? (Längd utstickande järn = 1,5 × Lb,rqd)
Svar: Avsnitt 8.7.2 är oklart formulerat och har föranlett många frågor.
Att man får skarva 100 % av armeringen i samma snitt om (3) uppfylls kan tyckas bli motsagt av andra strecksatsen i (3). Denna strecksats bör dock inte uppfattas som att skarvar alltid ska vara förskjutna, utan som en definition av vad som menas med att skarvarna är förskjutna; om skarvarna ligger närmare anses de således ligga i ”samma snitt”.
Villkoret för skarvning av 100 % i samma snitt bör således vara dels att armeringen ligger i ett lager, dels att första och tredje strecksatsen i (3) uppfylls. Härtill kommer att skarvlängden ska ökas med 50 % i förhållande till grundvärdet genom faktorn a6.
Publicerad 2017-05-30
Fråga: i SS-EN 1992-1-1 Bilaga J.2 finns figurer som visar armeringsutformning i ramhörn för stängande respektive öppnande moment. Kan ett ramhörn utformas enligt Figur J.4 (två överlappande U-järn) även vid stängande moment?
T ex om det öppnande momentet växlar till ett stängande momentet vid utbyggnadsskedet eller om utstickande järn vill undvikas mellan olika gjutetapper. Om överlappande u-järn inte är tillåtet vid stängande moment vad är i så fall teorin bakom detta?
Svar: Armering enligt figur J.3 b) skulle möjligen kunna fungera även vid stängande moment, men det förutsätter en direkt skarv mellan de båda slingorna. Skarvlängden skulle bli ungefär ¼ varv, minus avdrag för eventuellt avstånd mellan slingorna enligt regeln för ökning av skarvlängden enligt SS_EN 1992 kap 8.7.2 (3), vilket skulle förutsätta liten armeringsdiameter i förhållande till tvärsnittsdimensionerna.
Detta skulle möjligen kunna tillämpas i fall med små moment som kan växla riktning mellan öppnande och stängande.
Vid konsekvent stängande moment bör man följa rekommendationerna i J.2.2.
Publicerad 2017-05-30
Fråga: Vilka enheter ska användas på indata i formel B.116 i bilaga B, kapitel B.103.2?
Svar: Det bör vara samma enheter som i EN 1992-1-1, bilaga B, vilket betyder att fck sätts in i MPa, RH i %, t och ts i dagar samt h0 i mm.
Publicerad 2017-05-30
Fråga: Hur ska man gå tillväga för att handberäkna sprickbredder för höga balkar med armering?
Svar: Man kan beräkna krafter i dragband med fackverksmodell även i bruksgränstillstånd, och utifrån motsvarande armeringsspänningar beräkna sprickbredd. Svårigheten ligger i att välja en fackverksmodell som är lämplig i bruksgränstillstånd. Den enda vägledning man får i SS-EN 1992 är 5.6.4 (2), där det sägs att
”Verifieringar i bruksgränstillstånd får även göras med fackverksmodeller, t.ex. verifiering av armeringsspänningar och sprickbredder, om ungefärlig deformationskompatibilitet säkerställs (i synnerhet bör läge och riktning för viktiga trycksträvor överensstämma med linjär elasticitetsteori).”
Man bör iaktta viss försiktighet med att använda samma fackverksmodell som i brottgränstillstånd (såvida man inte även där har orienterat trycksträvor enligt linjär elasticitetsteori). I brottgränstillstånd kan man i vissa fall förutsätta trycksträvor med upp till 70 graders lutning i förhållande till dragbanden (se Betongföreningens handbok), men i bruksgränstillstånd kan man behöva förutsätta mindre vinklar, och i varje fall inte över 60 grader men inte flackare än 45 grader.
Publicerad 2017-05-30
Fråga: Vad gäller för minimiarmering (säkerhetsarmering) för oarmerat tvärsnitt i stadium 1(osprucket) - behöver vi att armera konstruktioner i denna nivå? Var man hittar det i Eurokoden?
Svar: För oarmerat tvärsnitt finns inget krav på minimiarmering. Om bärverksdelen uppfyller kriterierna i 12.1 (2) och om man kan uppfylla krav i brott- och bruksgränstillstånd så behövs ingen armering. Armering som kan behövas av andra skäl (t.ex. s.k. säkerhetsarmering, armering för lyft av väggelement m.m.) behandlas överhuvudtaget inte i SS-EN 1992.
Eftersom frågan tycks gälla väggar så kan det här också påpekas att SS-EN 1992 för närvarande. inte har någon användbar förenklad metod för ”handberäkning” av bärförmågan för oarmerade väggar. Det som står i 12.6.5.2 är oanvändbart eftersom det inte finns någon anvisning om hur man ska beräkna den i senare tillägg införda ”krypexcentriciteten” ej. Detta sätt att beakta krypning är överhuvudtaget inte lämpligt, om man vill ha hygglig noggrannhet utan alltför komplicerade uttryck. Förslag till bättre handberäkningsmetod har inlämnats från svensk sida.
Publicerad 2017-05-30
Fråga: Hur ska man se på en 100 mm tjock betongplatta till ett garage bredvid en villa? Det är trots allt en ganska vanlig konstruktion. Det finns flertalet knäckpunkter på vägen men frågeställningen är vilken armering som krävs i plattan med avseende på minimiarmering för att begränsa sprickvidderna.
Enl. 7.3.1 (1) i SS-EN 1992 ska sprickbildning begränsas. Och enl. tabell D-2 i EKS 10 ska sprickvidden begränsas med beroende på exponeringsklass, livslängdsklass samt armeringens korrosionskänslighet. Livslängdsklassen styrs av huruvida konstruktionen är åtkomlig för inspektion och underhåll eller inte enl. avdelning B 4§ i EKS 10. Här kommer första frågan, finns det någon armering som kan klassas som åtkomlig för inspektion och underhåll? Ska man därför betongplattan som L100? VI har svårt att se att många villor beräknas stå kortare än 50 år.
Nästa fråga är vilken exponeringsklass som man ska klassa ett garage för. Vi har dock svårt att få det till något annat än XD3. Stämmer det?
Om vi säger att vi får att betongplattan ligger i L100 så ska den, om vi använder föga korrosionskänsligt armering, och har exponeringsklassen XD3 ha en maximal beräknad sprickvidd till 0,15 mm.
Jag vill inte framstå som någon expert på området men jag har gjort ett gediget försök att räkna fram sprickvidden för en 100 mm tjock betongplatta till ett garage.
Jag har valt att se hela tvärsnittet som draget med centrisk armering. Är det korrekt? Täckskiktet blir således ganska stort. Jag har valt att begränsa stålspänningen ungefär enligt det förslag som finns i tabell 7.2N i SS-EN 1992 för sprickbredd 0,2 mm. I bifogat exempel har jag valt att börja med φ12 s100 vilket ger en stålspänning på 240 MPa. Detta ger enligt ekvation (7.1) i SS-EN 1992 en minimiarmering på 975 mm2.
När jag ska beräkna sprickvidden enligt ekvation (7.8) så får jag inte det att stämma. Lägger jag in φ12 s100 får jag en sprickbredd på 0,32 mm. Räknar jag om det med φ12 s50 får jag 0,248 mm. Räknar jag med φ16 s100 får spänningen ändras till 200 MPa vilket ger sprickbredden 0,271. Lägger jag in φ16 s50 får jag 0,207 mm. Det är ganska nära 0,2 men ändå inte 0,15 som är kravet enligt resonemanget ovan. Är inte φ16 s50 (4021 mm2/m) lite väl mycket armering för en garageplatta till en villa? Vår erfarenhet är att många liknande konstruktioner är armerade betydligt mindre armering. Men som jag ser det hittar jag inga förmildrande omständigheter i Eurokoden som gör att jag kan gå ner i armeringen.
En följdfråga blir ju om det ens går att få till en 100 mm garageplatta till en villa i XD3? Tar tacksamt emot förslag på hur i så fall.
Svar: Naturligtvis är ingen armering enkelt åtkomlig för inspektion, men detta betyder inte att golvet till ett villagarage måste dimensioneras i klass L100. Det handlar om konstruktionen, och en enkel inspektion kan vanligen avslöja om armeringen börjat rosta.
Lämplig exponeringsklass för golv i parkeringshus o.d. är normalt XD3, och om utrymmet inte är uppvärmt dessutom XF4. Sedan kan man kanske diskutera om man behöver ställa lika stora krav för ett enkelt villagarage, men om man vill ha samma livslängd bör man i princip göra det.
Tabell 7.2N i SS-EN 1992 är avsedd att vara ett förenklat alternativ till en beräkning av sprickbredd enligt 7.3.4. En spänning som kan utläsas ur den tabellen är inte alls avsedd att användas som grund för en sprickbreddsberäkning.
Om man vill beräkna sprickbredd på grund av last (moment) ska man använda den armeringsspänning som kan beräknas för sprucket tvärsnitt.
Om man vill beräkna sprickbredd på grund av centrisk dragning vid förhindrat tvång (t.ex. krympning) kan man använda en metod föreslagen i Svenska Betongföreningens Handbok till SS-EN 1992, sid 1-98. Den metoden är inte ”officiellt sanktionerad”, men kan användas i brist på bättre alternativ. Sprickbredden beräknad på detta sätt blir vanligen liten, men observera då att all beräkning av sprickbredder förutsätter att armeringen uppfyller minimikrav enligt 7.3.2; mindre armering än så kan i princip inte begränsa sprickbredd överhuvudtaget. Det blir därför 7.3.2 som bestämmer armeringsmängden.
Observera slutligen att viss ”lindring” av regeln i 7.3.2 har införts i EKS 10.
Publicerad 2017-05-30
Fråga: Är det verkligen meningen att alla takterrasser ska dimensioneras för en nyttig last på 5 kN/m2. Lasten är rimlig för ett gårdsbjälklag men för takterrasser borde en last nära balkonglasten vara högst rimligt. Har tidigare ställt frågan på ett litet annat sätt och fick då ett svar att det är upp till konstruktören att avgöra lasten. Men det är svårt i verkligheten att sätta en annan last än ni föreskriver.
Svar: Om takterrassen är att betrakta som en samlingslokal dimensioneras den för nyttig last enligt kategori C5. Den nyttiga lasten ges av SS-EN 1991-1-1, tabell 6.1. För svenska förhållanden motsvaras det av EKS 10, tabell C-1.
Enligt uppgift har frågan tidigare ställts till eurokodhelpdesk på ett lite annorlunda sätt. Då förutsattes takterrassen vara omgiven av kontor (kategori B). I detta fall är det inte rimligt att takterrassen har en nyttig last motsvarande kategori C5. För kontorslast finns inte någon last angiven för takterrasser. Det rimligaste är att använda last på balkonger för fall med takterrass. Enligt kap. 1.1.1, 9 § ska samma balkonglaster tillämpas för kategori B som för kategori A.
För stora areor får man även reducera nyttig last som är huvudlast enligt reduktion med αA, se kap. 1.1.1, § 9a.
Publicerad 2017-05-30
Fråga:

Svar:

Publicerad 2017-05-30
Fråga: Hur ska man räkna snedställningen för hela husets stabilitet med ett betonghus med endast betongväggar (SS-EN 1992-1-1 kap 5.2)?
Den horisontella kraften kan bara gå i riktningen vinkelrätt väggens plan. Så om man ska räkna ut horisontallasten i en riktning på ett dubbelsymmetriskt kvadratiskt hus så sätter man N (5.3ab) =Halva husets vertikalkraft. Stämmer påståendena?
Svar: Den vertikallast som bestämmer snedställningskraft i ena eller andra riktningen ska alltid vara hela vertikalkraften. En vägg kan även luta (eller ha någon annan icke avsedd excentricitet) i sitt eget plan, och ger då ett bidrag till snedställningskraften.
Publicerad 2017-05-30
Fråga: I Bro 2004 fanns regler för armering för uppkommande dragkrafter vid spännförankringar, så kallad sugarmering. I Bro 94 fanns även ett råd hur denna armering skulle beräknas. Jag har inte hittar någon motsvande formler för beräkning av sugarmering i Eurokod. Finns det några regler för sugarmering i Eurokod? Behövs inte denna armering enligt Eurokod?
Svar: Begreppet ”sugarmering” saknas i SS-N 1992-2. Det finns dock en regel i 8.10.4 (108) som behandlar spännförankringar inom en bärverksdel. Om det alltså inte finns en tryckspänning på minst 3 MPa så bör det läggas in armering för lokala dragspänningar bakom förankringen. Det ges inga anvisningar för beräkning av denna armering, men de gamla reglerna om” sugarmering” bör då kunna användas.
Publicerad 2017-10-19
Fråga: Jag har en fråga när det gäller en förstoringsfaktor på sprickbredd för en pålsula med en tjock täckskikt, 100 mm. Enligt Betonghandboken sida 409 "så långt sprickbreddsbegränsningen avser korrosionsskydd kan det i någon mån kompletteras av ett täckskikt större än enligt tabell 3-5 i BBK, t.ex genom att wk accepteras förstorad med faktor c/cmin, dock högst 1,5."
Finns det en förstoringsfaktor på sprickbredd enligt Eurokoden? Hur mycket blir det?
Svar: Det finns ingen särskild förstoringsfaktor för tillåten sprickbredd med hänsyn till täckskiktets storlek.
Täckskiktet får en viss inverkan på den beräknade sprickbredden genom värdet på rp,eff, som minskar med ökande täckskikt. I den svenska tillämpningen av sprickbreddsformlerna blir det ingen ytterligare inverkan av täckskiktet, men det kan nämnas att i det rekommenderade uttrycket för sprickavstånd tillkommer ytterligare en inverkan av täckskiktet genom termen 3,4c.
Kontentan är alltså att den beräknade sprickbredden ökar om man ökar täckskiktet, samtidigt som man inte tillåter större sprickbredd av den anledningen.
Publicerad 2017-10-19
Fråga: I SS-EN 1992-1-1 7.2 (2) anges att längsgående sprickor kan uppkomma om spänningsnivån under karakteristisk lastkombination överstiger ett kritiskt värde. Min fråga är hur ökningen av betongsskiktet i tryckzonen ska beräknas om kritiska värdet överskrids? I SS-EN 1992-2 7.2 (102) finns en begränsning av maximal ökning av spänningsgränsen vid omslutning. Varför finns det begränsning för broar och inte för byggnader?
Svar: Varken del 1-1 eller del 2 ger någon vägledning om hur mycket täckskiktet bör ökas för att man ska” slippa” spänningsbegränsningen till k1fck, eller hur mycket spänningen kan ökas över denna gräns om täckskiktet ökas med ett visst belopp. Det finns inga enkla svar på dessa frågor. (Ett enkelt svar är naturligtvis att ökat täckskikt kan ge ökad tvärsnittshöjd och därmed minskad spänning, men frågan handlar ju om hur man kan öka den tillåtna spänningen.)
Att spänningen genom omslutning kan ökas 10 % enligt del 2 bör kunna tillämpas även för husbyggnader. Se avsnitt 6.5.4 (5) i SS-EN 1992-1-1. Se även avsnittet ”Tilläggsinformation specifik för SS-EN 1992-2 och samband med SS-EN 1992-1-1” efter förordet i SS-EN 1992-2.
Publicerad 2017-10-19
Fråga: I SS-EN 1992-2 6.8 anges att utmattningsverifiering i allmänhet inte är nödvändig
för bropelare som inte är styvt förbundna med överbyggnaden. Är pelare med s.k.ofullständiga leder (med genomgående armering) att betrakta som "intestyvt förbundna med överbygganden?
Svar: Ja
Fråga: Är toleranser som anges i SS-EN 13670 med i de partialkoefficienter och säkerhetsfaktorer som används i SS-EN 1992-1-1? Exempelvis om vi har en fundamentsplint behöver vi räkna med ett extra moment av excentricitet av en bultgrupp i toppen som är 20 mm snett placerad enl. G.10.8 d SS-EN 13670?
Svar: De toleranser som är beaktade genom värden på partialkoefficienter för betong- och armeringshållfasthet är normala avvikelser för tvärsnittsmått, dvs inom normala toleranser enligt SS-EN 13670. Andra typer av avvikelser är inte beaktade. Exempel på sådana avvikelser är krokighet, lutningar och excentriciteter i pelare och väggar. Sådana avvikelser kan inte beaktas genom partialkoefficienter, utan måste alltid beaktas explicit. Ett annat exempel är felslagning av pålar.
Det aktuella exemplet skiljer sig från avvikelser i tvärsnittsmått, såtillvida att avvikelsen ger en excentricitet hos den kraft som angriper konstruktionen. Avvikelsen bör därför inte anses beaktad genom partialkoefficienter, utan bör beaktas explicit. Sedan kan det ju vara så att en excentricitet på 20 mm inte har någon stor inverkan i sammanhanget.
Fråga: Enligt tidigare svar enligt SIS gäller de tre begränsningarna 2,5(h-d), (h-x)/3 och h/2 i SS-EN 1992-1-1 7.3.2 (3) generellt för alla olika fall i figur 7.1, med undantag för att (h-x)/3 helt enkelt inte är relevant för c), då det där saknas tryckzon.
1. En fråga gäller hur höjden för den effektiva betongarean, hc,ef enligt 7.3.2 (3) och ρp,eff enligt formel (7.10) ska hanteras vid tunna tvärsnitt med stort täckande betongskikt respektive hårt belastade tvärsnitt med flera lager armering.
I några av dessa fall begränsas hc,ef av (h-x)/3 vilket medför att hela eller delar av armeringen ligger utanför hc,ef. Hur beräknas armeringsinnehållet As/Ac,eff enligt (7.10) om As är utanför området Ac,eff?
2. I figur 7.1 a visas en balk med flera lager armering där hc,ef synes vara större än (h-x)/3. Enligt tidigare svar från SIS gäller begränsningarna alla fall i 7.1. Är figuren felaktig?
3. Vad är tanken med att begränsa hc,ef då den mindre av begränsningarna synes minska Ac,eff vilket torde ge ett högre armeringsinnehållet rå,eff vilket minskar sprickbredden?
4. Är det tillåtet att betrakta delar av ett tjock täckande betongskikt som overksamt vid beräkning av sprickbredder? Då betongen är uppsprucken påverkas inte armeringsspänningen och tryckzonen med däremot flyttas hc,ef uppåt i kan ge att fler lager armering får plats inom Ac,ef.
Följdfråga: I svaret till första frågan står:
Även armering som hamnar utanför den effektiva betongarean kan medräknas (så länge den ligger i dragen zon). Den effektiva betongarean är inte någon verklig area, bara en referensarea för beräkning av ρp,eff.
Intuitivt känns det lite tveksamt att all armering, även den som ligger nära neutrala lagret, får medräknas i effektiva armeringsinnehållet och därmed reducera sprickbredden. Jag har sökt i litteraturen , fib Bulletin 52 avsnitt 4.3.2, och hittat lite teori för beräkning av sprickbredder.
I bulletinen står det "The reinforcement controlls cracks widths only within a small area around the bars. This area is defined as the effective concrete area in tension, Ac.ef. In flexural members, a general approach is to take an area of concrete surrounding the main steel and having the same centroid as the steel as A.cef."
Om jag förstått härledningen, som görs med jämvikt mellan vidhäftning, dragen betong, dragen armering och övriga villkor, bör As endast vara den armeringsarea som är inom Ac.ef och inte all armering i dragzonen.
I bulletinen redovisas även en formel för sprickbredd och där anges Ac.eff som den betongarea som omger den dragna armeringen inom h.cef.
Är det lämpligt att medräkna all armering i dragzonen med tanke på vad anges i den teoretiska bakgrunden i fib Bulletin 52 ?
Vid tvärsnitt med många armeringslager, där t ex (h-x)/3 begränsar h.cef, kan man få väldigt höga värden på ρp,eff (om all armering i
dragzonen medräknas) och därmed små sprickbredder.
Svar: 1. Även armering som hamnar utanför den effektiva betongarean kan medräknas (så länge den ligger i dragen zon). Den effektiva betongarean är inte någon verklig area, bara en referensarea för beräkning av .
2. Figuren är slarvigt ritad, begränsningen till (h-x)/3 gäller.
3. "Tanken" med att begränsa hc,ef torde vara att beräknade sprickbredder ska stämma bättre med försöksresultat. Beräkningsmetoden är i huvudsak empirisk, och vissa saker kan då inte förstås eller förklaras på annat sätt.
4. Vid tjockt täckskikt kan begränsningarna (h-x)/3 eller h/2 bli styrande, varvid den effektiva betongarean inte påverkas av täckskiktet. Någon annan "borträkning" av täckskikt är inte aktuell.
Svar på följdfråga: I citatet ur fib Bulletin 52 talas om en effektiv betongarea som generellt kan tas som den omslutande betongarea som har samma tyngdpunkt som armeringen. Detta är samma definition som grunddefinitionen i BBK 04, innebärande att effektiva betongareans höjd vid rektangulär dragzon blir 2 ggr avståndet från dragen kant till armeringens tyngdpunkt. I SS-EN 1992 har detta modifierats till en något större area, med höjd = 2,5 ggr avståndet till armeringens tyngdpunkt. Dessa definitioner av effektiv betongarea kan i viss mening ges en fysisk tolkning.
Både BBK och SS-EN 1992 har därutöver en begränsning av effektiva betongareans höjd till ((h-x))⁄3. Denna begränsning har veterligen ingen direkt fysisk innebörd, utan kan antas ha tillkommit för att bättre anpassa beräknade sprickbredder till försöksresultat. Se punkt 3 i det tidigare svaret på fråga 568.
Om denna begränsning blir avgörande kan det hända att viss armering hamnar utanför den effektiva betongarean. Det finns dock ingenting i vare sig EK2 eller fib Model Code 2010 som säger att bara armering inom höjden ((h-x))⁄3, dvs inom den nedre (vid drag i underkanten) 1/3-delen av dragzonen, skulle få medräknas. Även dragen armering ovanför denna nivå bör kunna påverka sprickbredden, åtminstone inom höjd enligt grunddefinitionen.
Fråga: Vid kontroll, om skjuvarmering behövs, med avseende på genomstansning för en pålad platta (enligt avsnitt 6.4) med ett applicerat moment från vindlast som yttre last har det dykt upp lite funderingar.
Kontrollen avser ett hörn som förenklat kan liknas med figur 6.15 längst till höger. Vid kontrollen enligt 6.4.4 är V(Ed) enligt ekvation 6.51 > än V(Rd,c) enligt ekvation 6.47. Ekvation 6.47 är slående lik ekvation 6.2.a i avsnitt 6.2.2 bortsett ifrån att den här ges i kN istället för MPa. Dock finns ett minsta värde enligt ekvation 6.2.b givet för ekvation 6.2.a.
D.v.s, om kapaciteten enligt 6.2.a är lägre än kapaciteten enligt 6.2.b så gäller den sistnämnda? Kan samma minsta värde (där bw ersätts med u) användas för kontroll av genomstansning? I mitt fall så är V(Rd,c) enligt 6.47 multiplicerat med u x d lägre än V(Rd,c) enligt 6.2.b där bw ersatts med u och jag är därför osäker på om jag kan resonera så och isåfall slipper skjuvarmering med avseende på stansningen här.
Svar: Undre gränsen v_min enligt ekvation (6.3N) gäller även vid stansning, se ekvation (6.47) samt ANM i 6.4.4 (2).
Det kan tilläggas att ekvation (6.51) för att beakta excentricitet gäller för en grundplatta med excentrisk pelarlast, och inte för en påle i hörnet på en pålad platta. Istället är det ekv (6.39) som gäller (den ger dock samma resultat för givet kontrollsnitt).
Fråga: När det kommer till tvärkraftsarmering i grundplattor så har jag problem med att tolka koden när det kommer till lutande tvärkraftsarmering i ett fåtal lager. Säg att jag vill lägga in lutande tvärkraftsarmering i form av G-järn med lutningen 45 grader i ett eller två lager.
Kan jag då använda VRd,s =ASW*fywd(cot θ + cot α)sin α, som ger för 16 mm armering med avstånd 250 mm = 806 mm2 x 435 x (1.5+1) x 0,7 =613 kN (med cot θ =1.5 och 45 grader och ett lager). Eller ska jag använda VRd,s =ASW x fywd x sin α = 806 x 435 = 350 kN (samma förutsättningar som ovan)?
Som jag tolkar det kan jag egentligen inte använda den första formeln för beräkning av enskilda stänger, men då blir resultatet att jag alltid ska tvärkraftsarmera med byglar i 90 grader för det blir bättre kapacitet, men så är väl inte i verkligheten? Eller får jag använda cot θ faktorn även på ett fåtal stänger? Blir mer rimliga värden på kapaciteten och det stämmer bättre med tidigare koder. Har en formel från betonghandbogen (16b sid 246) som ger en faktor på √2 för armering som ligger med 45 graders vinkel. Hur får jag med denna faktor i den nya koden och kan jag få med detta för armering som ligger i ett fåtal lager? Gör det någon skillnad rent formel mässigt om jag lägger armeringen i två lager?
Svar: Det är OK.
Fråga: Beaktar Eurokoden sprickarmering för att begränsa sprickor uppkomna pga. krympning i betongen, d.v.s helt obelastade tvärsnitt, t.ex. en platta på mark? 7.3.1 (3) säger något i frågan men vi tycker det är lite oklart om det betyder att metoderna i Eurokoden inte gäller för att begränsa den typen av sprickor? Om metoderna i Eurokoden gäller, hur räknar man i så fall ut spänningen i armeringsstängerna precis efter uppsprickning? Och är det samma spänning som ska användas i ekvation 7.1 och 7.9?
Svar: SS-EN 1992-1-1 ger ingen direkt vägledning för beräkning av sprickbredd till följd av förhindrad krympning.
Om det gäller att begränsa sprickbredden till ett visst värde kan man använda ekvation (7.1) med en spänning enligt avsnitt 7.3.3, men denna spänning ska aldrig användas för direkt beräkning av sprickbredd enligt 7.3.4, ekvation (7.9) m.fl. Metoden i avsnitt 7.3.3 ger ofta mycket konservativa resultat.
Om det gäller att beräkna sprickbredd på grund av förhindrad krympning kan man istället använda en metod som föreslås i Svenska Betongföreningens Handbok till Eurokod 2 (Betongrapport 15), sid 1-98. Andra modeller för detta ges i EN 1992-3. Dessa metoder bygger på att man i sprickbreddsformeln (7.9) sätter in en töjning som är mer eller mindre beroende av krympningen.
Fråga: Vid beräkning av genomstansning enligt avsnitt 6.4.3 påverkar betafaktorn kraftigt kapaciteten. Hur påverkas denna vid ledad pelare? Vilket moment avses i ekvation 6.39, pelarens eller plattans? Om det är plattans, vilken riktning avses?
Svar: Excentriciteten kan normalt tas som det moment som överförs till pelaren (M) dividerat med pelarlasten (V), dvs M/V. Riktningen är den riktning som momentet verkar i. Om det finns moment i två huvudriktningar blir det riktningen för det resulterande momentet.
Vid ledad pelare skulle detta innebära att det aldrig blir någon excentricitet, men så är inte fallet. Även här kan skjuvspänningen i kontrollsnittet bli ojämnt fördelat på grund av excentricitet, men denna måste då tas fram på annat sätt. Ett sätt kan vara att ur en FEM-beräkning ta fram tvärkraftens fördelning i kontrollsnittet. Ett annat sätt kan vara att ur en "handberäkning" av plattan, t.ex. med strimlemetod, ta fram det obalanserade momentet i respektive riktning, på ett avstånd från pelaren svarande mot kontrollsnittet.
Fråga: Enligt kontrollants bedömning är att distanslister inte bör användas på vertikala ytor. Vad gäller för användandet av distanslinjaler? Räknas täckskiktet med som bärande del i en betongkonstruktion? Vad gäller generellt för täckskikt I betongkonstruktioner.
Svar: För att ta den sista frågan först: Det som gäller generellt för täckskikt står i SS-EN 1992 avsnitt 4 och Boverkets EKS 10.
Huruvida täckskikt räknas med i bärande tvärsnitt beror på omständigheterna. Täckskikt i dragzon räknas inte med vid analys av sprucket tvärsnitt, vare sig i bruks- eller brottgränstillstånd. Täckskikt i tryckzon, eller i dragzon vid analys av osprucket tvärsnitt, räknas däremot med.
Distanslister är en utförandefråga, som något behandlas i SS-EN 13670. Där står bl.a. att långa kontinuerliga distansanordningar som kan initiera sprickor är olämpliga i korrosiva miljöer. Horisontella distanslister bör naturligtvis inte användas på vertikala ytor.
Fråga: 1- Jag håller med att sprickkriteriet med svensk tillämpning fctk/ζ enligt EKS, gäller för spännbetong. Jag håller med även att man räknar deformationer med draghållfasthet fctm.
Däremot när det gäller slakarmerad betong beskrivs att draghållfasthet 0 som ska användas. Jag tycker att det är ganska dåligt formulerat i EKS vilket göra att människor misstolkar regler.
2- Stycke från EKS:
”Stycke 7.3.1(5) Allmänt råd 20 § Såvida inte något annat kan anses vara motiverat bör värdet på wmax beräknat för kvasi-permanent lastkombination begränsas till värdet enligt tabell D-2. Om dragspänningen inte överstiger fctk/ζ kan betongen anses vara osprucken. Värden på spricksäkerhetsfaktorn ζ enligt tabell D-3 bör tillämpas. För frekvent lastkombination ställs inga krav på sprickbreddsbegränsning.”
3- Om jag förstår Eurokod rätt så gäller avsnitt 7.3.1 gäller allmänt. Detta betyder att man pratar inte speciellt om spännbetong eller nåt annat. Min fråga är varför meningen ” Om dragspänningen inte överstiger fctk/ζ kan betongen anses vara osprucken.” ligger under stycke 7.3.1(5) om detta gäller endast för spännbetong. Det är väldigt många konstruktörer som använder sprickkriteriet med svensk tillämpning fctk/ζ för slakarmerad betong bara på grund av den meningen.
Svar:1- Svaret att draghållfasthet 0 gäller för slakarmerad betong syftar på 7.3.2 (1)P, enligt vilket minimiarmering fordras där det förekommer dragspänning (och om det finns krav på sprickbreddsbegränsning). Det betyder att gränsen för krav på minimiarmering går vid dragspänning 0 för slakarmerad betong; för spännbetong går motsvarande gräns vid fctk/z.2- Stycket 7.3.1 (5) handlar inte om minimiarmering, utan om huruvida sprickbredden bör begränsas till till ett visst värde eller inte. Gränsen för behovet av sådan sprickbreddsbegränsning går alltså vid dragspänning fctk/ζ, och det gäller både slakarmerad och förspänd betong.
3- Om dragspänningen inte överstiger fctk/ζ finns inte behov av begränsning av sprickbredd till ett visst värde. Däremot skulle man ju kunna ha ett mer allmänt krav på sprickfördelning, så att armeringen inte flyter i den första spricka som slår upp. I så fall kan det kanske vara aktuellt med minimiarmering enligt avsnitt 7.3.2 för en slakarmerad konstruktion, även om dragspänningen ligger mellan 0 och fctk/ζ.
Fråga: För att begränsa sprickorna i en betongkonstruktion kan man använda tabell 7.2N och 7.3N i SS-EN 1992. I svenska betongföreningens handbok vol.1 står det under 7.3.3 att tabellvärdena är beräknade så att resultat på säkra sidan erhålls i de flesta fall och att det kan löna sig att göra en beräkning enligt 7.3.4. Under 7.3.4 i samma handbok presenteras en metod för att beräkna sprickbredd pga förhindrad krympning.
Problemet är att det verkar som att 0,6 x betongens krympning alltid blir större än det andra villkoret eftersom det alltid blir negativt, vilket i så fall innebär att sprickbredden blir densamma oavsett om man använder betong C16/20 eller C50/60. Det kan väl inte vara rätt? Kan det vara så att det är absolutbeloppet av de båda uttrycken man ska använda?
Svar: Det är inte meningen att absolutbeloppet ska användas. Det blir mycket riktigt så att begränsningen 0,6 x krympningen praktiskt alltid blir avgörande, och då spelar betongens hållfasthet m.fl. parametrar ingen roll. Det beror på att gränsen 0,6 etc är grov och ganska godtycklig. I BBK fanns en liknande gräns, som då var 0,4.
Det är också så att metoden i 7.3.4 i första hand är avpassad för sprickbredd på grund av last, och inte för förhindrad krympning. Metoden i Betongföreningens handbok är ett förslag som kan gavs i brist på annat. Det finns dock andra modeller i SS-EN 1992-3.
Metoden i Betongföreningens handbok ger i vissa fall för liten beräknad sprickbredd. En armering som uppfyller minimivillkoret enligt ekv (7.1) med armeringsspänning fyk har visat sig kunna ge sprickbredder av förhindrad krympning som är större än vad de högre exponeringsklasserna tillåter, men som kan vara acceptabla om det inte finns krav med avseende på beständighet, funktion eller estetik, och om den enda inverkan är förhindrad krympning.
Om det finns krav på sprickbreddsbegränsning bör tillsvidare minimiarmeringsvillkoret (7.1) tillämpas med en begränsad spänning enligt tabell 7.2N. I så fall är det viktigt att justera stångdiametern enligt ekv (7.7N). I ekv (7.7N) ska för övrigt ingå en faktor k1 = 0,8 i täljaren. För att få fram aktuell spänning ska omräkningen tillämpas "baklänges", dvs man går in i tabellen med ett omräknat f*.
Fråga: Fråga gällande sprickviddsberäkning enligt 7.3.4 (3) vid beräkning av Sr, max. Undrar över faktor k2 som beaktar tvärsnittets töjning. För en enkel platta i böjning med eller utan normalkraft i drag eller tryck så råder inga tvivel.
Men vad gäller för sammansatta sektioner? Vad gäller för I och T-tvärsnitt? I fallet med en vägg ihopgjuten med en underliggande platta som utsätts för böjning kommer hela medverkande plattan vara dragen, men totala tvärsnittet vara utsatt för böjning. Vid beräkning av k2 för plattan skulle 7.13 kunna tillämpas, men var antas tvärsnittets kanter vara?
Om hela sektionen beaktas kommer den övre kanten vara tryckt och k2=0,5. Om plattans ovankant ska betraktas som tvärsnittets ena kant kommer k2 anta ett värde närmre 1,0.
Svar: Om tvärsnittet antas fungera som ett T-tvärsnitt med dragen fläns så skulle man formellt sett, utifrån definitionen av k2, kunna använda k2 = 0,5, eftersom det är fråga om ren böjning. Det finns ingenting som säger att detta skulle vara knutet till någon speciell tvärsnittsform.
Om man istället utgår från att plattan i sin helhet är dragen så skulle man sätta k2 = 1,0.
Som en lämplig kompromiss kan man istället utgå från formuleringen "För fall med excentrisk dragkraft eller för lokala områden...". Man skulle då beräkna töjningsfördelningen för osprucket tvärsnitt, och sedan beräkna k2 enligt ekvation (7.13) med e2 = töjningen i plattans översida.
Fråga: Var går gränsen mellan innerpelare och kant/hörnpelare? Enligt 6.4.2(4) så klassas pelaren som kant/hörnpelare om kontrollsnittet begränsat av fri kant, underskrider grundkontrollsnittet. Det här innebär att pelaren kan stå långt in från kanten men ändå klassas som kant/hörnpelare. Då det reducerade kontrollsnittets längd, enligt figur 6.20, begränsas av MIN(1.5d;0.5C), (antar här att C är avståndet till fri kant?) så ger detta extrema värden på excentricitetsfaktorn enligt formel 6.44 och 6.46, för en pelare som står långt in från kanten. Hur skall man tolka detta?
Svar: Gränsen mellan innerpelare och kantpelare går just så som det beskrivs i frågan.
För kantpelare som uppfyller villkoren i 6.4.3 (4), dvs excentricitet vinkelrätt mot kanten riktad in mot plattan (vilket ju är det normala), och ingen excentricitet parallellt med kanten, kan man dock förutsätta jämnt fördelad skjuvkraft längs det reducerade kontrollsnittet u1* och excentricitetsfaktor behöver då inte användas. Den excentricitetsfaktor som definieras i ekvation (6.44) gäller för excentricitet parallellt med kanten.
Beträffande måttet c1 så bör det tolkas som avståndet mellan plattans kant och pelarens innerkant. Detta stämmer med definitionen i ekvation (6.41) om pelaren står kant i kant med plattan. Det ger rimligt resultat även om pelaren står innanför kanten, eller om den sticker utanför kanten (i figur 9.9 a) bör c1 alltså motsvara måttet y, inte cy).
2: Enligt 6.4.1(5) får stanskraften reduceras med motriktad jämnt fördelad last inom kontrollsnittet, för tex. grundplattor. Vad menas här med tex.? Kan detta vara aktuellt även för bjälklagsplattor med mycket överfyllnad?
Svar: Enligt 6.4.3 (6) kan man mycket riktigt välja en excentricitetsfaktor 1,5 för hörnpelare, vilket då innebär en övre gräns för vad man behöver förutsätta, om ekvation (6.46) ger ett högre värde. DeBeträffande 6.4.1 (5) så talar man i den engelska texten om ”special cases, such as footings”. För grundplattor tillkommer dock speciella regler i 6.4.4 (2), bl.a. innebärande att man, förutom att dra bort grundtryck innanför kontrollsnittet, även bör beakta kontrollsnitt närmare pelaren än 2d, vilket ofta blir avgörande trots att man då kan öka skjuvhållfastheten (se t.ex. exempel F i Svenska Betongföreningens handbok till SS-EN 1992).
Dessa regler är inte avsedda att användas för bjälklag, där man vanligen endast beaktar ett kontrollsnitt 2d utanför pelaren. Kontrollsnittet är en beräkningsparameter, som valts att ligga 2d utanför pelaren för att man ska få i princip samma ”skjuvhållfasthet” som vid ”vanlig skjuvning”. Last innanför detta fiktiva snitt bidrar också till det koncentrerade tryck runt pelaren i plattans underkant, som styr bärförmågan vid genomstansning.
Motiv till olika regler är bl.a. att i en grundplatta omfördelas grundtrycket i gynnsam riktning vid plattans deformation, vilket inte är fallet med lasten på ett bjälklag.
Fråga: I svaret nedan förklaras vilka sprickkriterier som bör användas i Sverige. Frågan var ställd angående generella fall men däremot är svaret specifikt för spännbetong. Jag undrar om svaret fctk/ksi gäller även för samtliga betong konstruktioner. Nedan kopierar jag till refererad frågan och svar. Fråga: Det råder en viss förvirring när det gäller när betong spricker enligt SS-EN 1992 åtminstone i Sverige. I normen gäller generellt att sprickkriteriet är fctm eller fctm,fl om sektionen endast är utsatt för böjning. Sedan finns det i svenska annexet kriteriet fctk/ksi där ksi beror av miljö och livslängdsklass. Frågan är vilket som skall användas? I Betongföreningens handbok SS-EN 1992 volym I avsnitt 7.1 kan man läsa: "Värdet fctk/ksi som gräns för uppsprickning bör väljas generellt när det gäller att med viss säkerhetsmarginal undvika sprickor men om det gäller att göra mer sannolika bedömningar av betongens uppsprickning t.ex. vid beräkning av deformationer kan man istället välja fctm eller fctm,fl." Att det finns två olika kriterier skapar alltså en viss förvirring. Hur bör man tänka i det här fallet?
"SS-EN 1992-1-1 Uppsprickning av betong
Fråga: Det råder en viss förvirring när det gäller när betong spricker enligt SS-EN 1992 åtminstone i Sverige. I normen gäller generellt att sprickkriteriet är fctm eller fctm,fl om sektionen endast är utsatt för böjning. Sedan finns det i svenska annexet kriteriet fctk/ksi där ksi beror av miljö och livslängdsklass. Frågan är vilket som skall användas? I Betongföreningens handbok SS-EN 1992 volym I avsnitt 7.1 kan man läsa:
"Värdet fctk/ksi som gräns för uppsprickning bör väljas generellt när det gäller att med viss säkerhetsmarginal undvika sprickor men om det gäller att göra mer sannolika bedömningar av betongens uppsprickning t.ex. vid beräkning av deformationer kan man istället välja fctm eller fctm,fl."
Att det finns två olika kriterier skapar alltså en viss förvirring. Hur bör man tänka i det här fallet?
Svar: Det som står i Betongföreningens handbok är väl klart nog, men det är egentligen bara en kommentar till vad som även kan utläsas ur SS-EN 1992. För att avgöra eventuellt behov av sprickarmering i spännbetong gäller fctk/ksi enligt den svenska tillämpningen av SS-EN 1992, 7.3.2 (4) . För beräkning av deformationer använder man däremot normalt fctm eller fctm,fl, vilket framgår av 7.4.3 (4)."
Svar: Sprickkriteriet enligt 7.3.2 (4), med svensk tillämpning fctk/z enligt EKS, gäller mycket riktigt för spännbetong; minimiarmering behövs om dragspänningen överstiger detta värde, och om det dessutom finns krav på sprickbreddsbegränsning.
För slakarmerad betong gäller i stället att minimiarmering krävs om det överhuvudtaget finns dragspänning, se 7.3.2 (1)P, och om det dessutom finns krav på sprickbreddsbegränsning. Man kan säga att sprickkriteriet här är draghållfasthet 0.
Här vill man inte riskera att missa minimiarmering genom att överskatta betongens draghållfasthet. För slakarmerade konstruktioner är man då extra försiktig, bl.a. eftersom uppsprickning kan medföra grova sprickor om minimiarmering saknas. Detta är normalt inte fallet i spännbetong, där övergången mellan osprucket och sprucket stadium sker mera gradvis.
När man beräknar deformation vill man i regel få en så sannolik uppskattning av deformationen som möjligt, och vid en noggrann beräkning tar man hänsyn till att konstruktionen kan vara sprucken i vissa delar och osprucken i andra, beroende på dragspänningen i förhållande till förutsatt draghållfasthet. Förutsatt draghållfasthet har även viss betydelse genom parametern z i ekvation (7.18-19). Att förutsätta en lägre draghållfasthet än (eller ) kan här leda till en systematisk överskattning av deformationen (förutsatt att man även beaktar krympning m.m.). Det är detta som åsyftas i Betongföreningens Handboks formulering om "sannolika bedömningar".
Kriteriet för betongens uppsprickning kan således vara olika i olika sammanhang, och det är ingen svårighet att särskilja de olika fall som beskrivs ovan.
Vi lever i en värld av förkortningar.
I SIS förkortningsordlista hittar du de allra vanligaste förkortningarna som används i standardiseringssammanhang.
SS-EN 1990 – Grundläggande dimensioneringsregler
SS-EN 1992 – Betongkonstruktioner
SS-EN 1993 – Stålkonstruktioner
SS-EN 1994 – Samverkanskonstruktioner i stål & betong
SS-EN 1995 – Träkonstruktioner
SS-EN 1996 – Murverkskonstruktioner
SS-EN 1997 – Geokonstruktioner
SS-EN 1998 – Jordbävningsresistenta konstruktioner